Skip to content

17 概念详解：通过相似度模糊检索

你好，我是叶伟民。

第15节课我们讲到了向量和相似度。我们以后面这五个事物为例，讲解了如何使用嵌入模型获得具体的向量值：

  1. 老婆饼
  2. 老婆
  3. 夫妻肺片
  4. 菠萝
  5. 菠萝包

上一节课，我们又学习了如何使用向量数据库存储、更新、删除以上向量值。今天我们就来看看，向量值在RAG里的应用，通过计算向量值的相似度来检索知识，这也是RAG检索的核心。

RAG检索的核心——相似度计算

我们先来看这样一个检索案例。

用户输入：我想吃一个老婆饼
系统从数据库里面检索到老婆饼数量为0
然后系统从其他四个事物中检索出一个并返回如下回答
系统回答：老婆饼没有了，我们有__，你需要吗？

那么问题来了。这时候，我们的应用如何从其他四个事物找出“菠萝包”来填充上面的空白之处呢？

相信细心的同学估计已经找到了答案，就是根据相似度进行查找（如果印象不深了可以回看第15节课）。换句话说，就是计算四个事物中与“老婆饼”的距离，再返回距离最近的那个。

那么这个距离应该如何计算呢？这就需要我们了解计算距离的几个方法。

  1. L1距离（曼哈顿距离）
  2. L2距离（欧几里得距离）
  3. 负内积（Negative Inner Product）
  4. 余弦距离（Cosine Distance）

L1距离（曼哈顿距离）

首先我们来看L1距离，它还有一个名字叫曼哈顿距离。那为什么会有这样一个名字呢？

想象一下，你在纽约市曼哈顿区驾驶汽车，如果你只能沿着街道（东西向或南北向）直行，不能斜穿街区，那么你从一个街区的A点走到另一个街区的B点（例如从下图的点[0, 0]驾驶汽车去点[5, 6]），最短的行驶距离是多少呢？

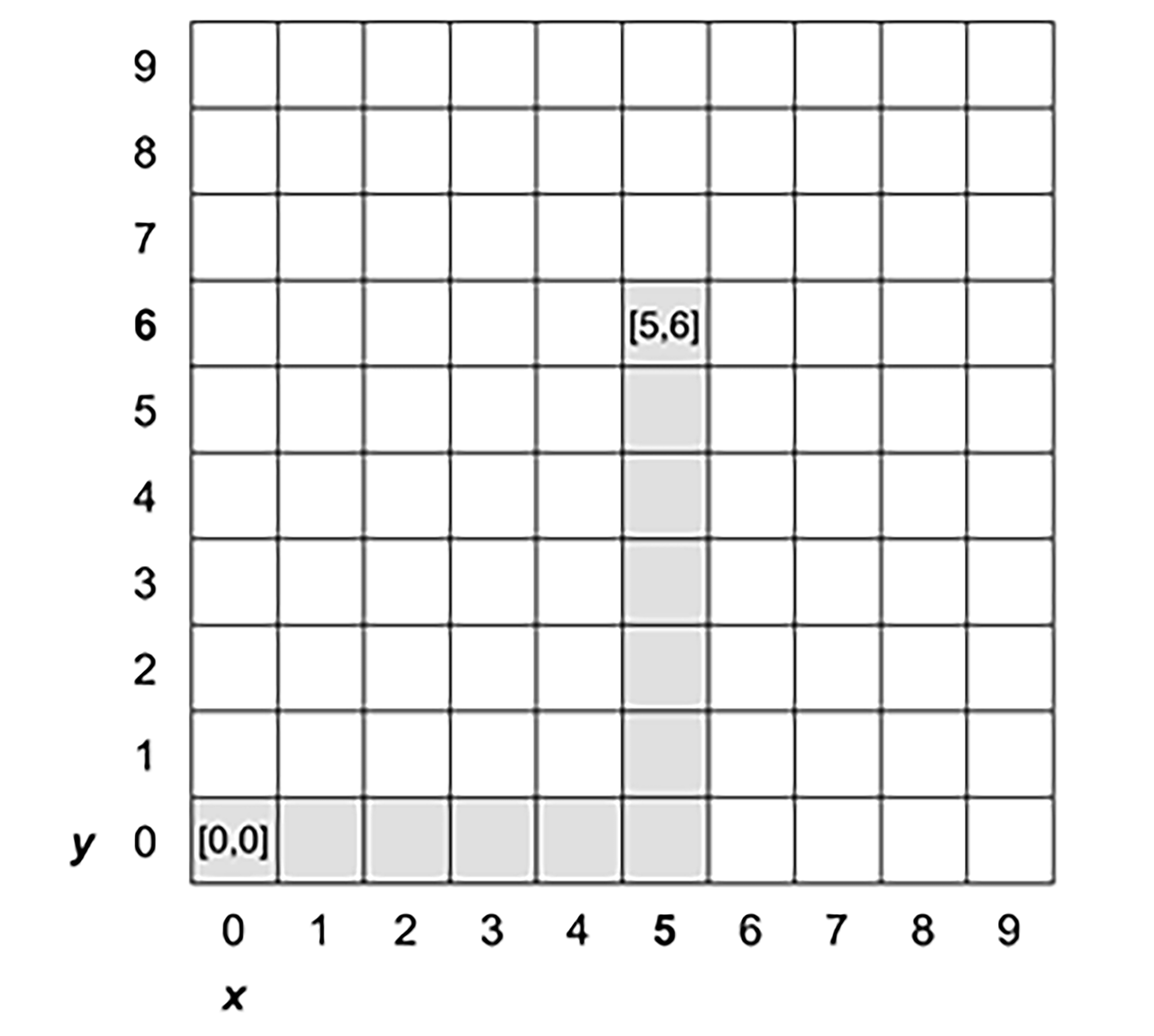显然，按照上述规则，我们从A到B的最短路径就是先沿着X轴行驶，然后沿着y轴行驶。然后将这两个距离相加，就是曼哈顿距离（L1距离）了。

看完了这个例子之后，我们再来看L1距离的定义就很好理解了**。L1距离 是指两个点在标准坐标系上绝对轴距的总和。

适用场景

L1距离对每个维度的权重是相同的，这有助于捕捉文本中各个特征的独立贡献。

所以当你的NLP任务需要考虑文本特征的独立贡献，选择L1距离可能会比较合适。这样说可能有点抽象，我给你提供几个具体场景辅助你理解。

下面这几个场景里，就比较适合计算L1距离。

  1. 产品评论分析： 在分析客户对产品的评价时，某些关键词可能对情感判断有显著影响。例如，“令人失望”“非常满意”或“性能卓越”等短语可能直接影响评论的情感分类。

  2. 品牌监测： 企业可能希望监测社交媒体上提及自己品牌的情感。在这种情况下，与品牌相关的特定话题或特征词（如产品特性、价格、客户服务等）的独立贡献可能对分析结果至关重要。

  3. 医疗咨询分析： 在分析患者对医疗服务的反馈时，特定的医疗术语或患者体验描述可能对判断患者满意度有显著影响。

因此就我们的“老婆饼”和“老婆”“菠萝”和“菠萝包”的示例而言，其实是适合使用L1距离的，因为这些都是特定的关键词。

具体实现

我们的课程使用了向量数据库是pgvector，L1距离在pgvector里面对应的运算符是 <+>。

以下是使用L1距离计算示例中其他事物与“老婆饼”相似度的代码。

SELECT 向量编码 <+> (SELECT 向量编码 FROM 事物 where name='老婆饼') AS 距离 FROM 事物;

L1距离在LangChain里面的实现是这样的：

from langchain.evaluation import EmbeddingDistance, load_evaluator

# 加载 embedding_distance 评估器，并指定使用 L1 距离
evaluator = load_evaluator("embedding_distance", distance=EmbeddingDistance.MANHATTAN)

# 评估两个字符串的语义相似度
evaluator.evaluate_strings(prediction="I shall go", reference="I will go")

L2距离（欧几里得距离）

L2距离是最直接的，也是我们日常生活中最直观的距离概念，就是指两点之间的直线距离。

例如一张纸上有两个点，想要知道这两个点之间的最短路径，你只需要简单地用一条直线连接它们，然后量出这条线段的长度，这个长度就是L2距离。因为欧几里得在其著作《几何原本》中定义了这种距离，所以L2距离又称欧几里得距离。

适用场景

L2距离适合文本聚类。例如我们要将以下事物进行分类：

  1. 老婆饼
  2. 老婆
  3. 夫妻肺片
  4. 菠萝
  5. 菠萝包

那么我们可以使用L2距离。

具体实现

向量数据库pgvector里面，L2距离对应的运算符是 <->。

以下是使用L2距离计算示例中其他事物与“老婆饼”相似度的代码。

SELECT 向量编码 <-> (SELECT 向量编码 FROM 事物 where name='老婆饼') AS 距离 FROM 事物;

L2距离在LangChain里面的实现是这样的：

from langchain.evaluation import EmbeddingDistance, load_evaluator

# 加载 embedding_distance 评估器，并指定使用 L2 距离
evaluator = load_evaluator("embedding_distance", distance=EmbeddingDistance.EUCLIDEAN)

# 评估两个字符串的语义相似度
evaluator.evaluate_strings(prediction="I shall go", reference="I will go")

我们可以看到，与L1距离相比，代码基本是一样的，区别只是在load_evaluator函数里面将distance参数改为了EmbeddingDistance.EUCLIDEAN。

负内积

负内积（Negative Inner Product，简称NIP）比较抽象，而且因为后面介绍的余弦距离更适合RAG，同时LangChain目前也没有支持负内积的API，所以这里我们就简单描述一下。

计算负内积需要分两步完成：

  1. 计算两个向量之间的点积。
  2. 求上一步内积计算结果的相反数。

适用场景

负内积适用于以下NLP任务。

  1. 主题建模：在主题建模中，负内积可以作为衡量文档向量与潜在主题向量之间差异的方法。

  2. 文本分类：在文本分类任务中，负内积可以用于计算文本向量与各类别向量之间的不相似度，辅助分类决策。

  3. 情感分析：情感分析其实算是文本分类的一个变种，只不过其文本分类的类别更少（积极、中性、消极）。

  4. 文档去重：在文档去重任务中，负内积可以衡量文档向量之间的差异，帮助识别重复或相似的文档。

具体实现

负内积在向量数据库pgvector里面对应的运算符是 <#>。

以下是使用负内积计算示例中其他事物与“老婆饼”相似度的代码。

SELECT 1-(向量编码 <#> (SELECT 向量编码 FROM 事物 where name='老婆饼')) AS 距离 FROM 事物;

注意，与前面的L1距离和L2距离相比，我们需要用1减去运算符计算出的结果。

负内积距离在LangChain里面的实现如下。

from langchain.evaluation import EmbeddingDistance, load_evaluator

# 加载 embedding_distance 评估器，并指定使用 L1 距离
evaluator = load_evaluator("embedding_distance", distance=EmbeddingDistance.MANHATTAN)

# 评估两个字符串的语义相似度
evaluator.evaluate_strings(prediction="I shall go", reference="I will go")

比较遗憾的是，到今天为止，LangChain还没有支持负内积计算的API，所以我们只能自己实现了。

from langchain_community.vectorstores.utils import DistanceStrategy
# 假设我们已经有了两个向量vec1和vec2
vec1 = [1, 2, 3]
vec2 = [4, 5, 6]

# 计算点积
dot_product = sum(a * b for a, b in zip(vec1, vec2))

# 计算负内积距离
negative_inner_product_distance = -dot_product

print("负内积距离:", negative_inner_product_distance)

不过LangChain更新很频繁，说不定明天就有支持负内积计算的API了。

余弦距离

余弦距离（Cosine Distance）是通过计算两个向量的余弦相似度来衡量它们之间的差异。

具体来说分两步，首先计算两个向量的余弦相似度，然后使用1减去余弦相似度。

余弦距离的值越小，就表示两个向量越相似。

余弦距离具有以下特点：

  1. 余弦相似度关注的是向量的方向而非大小，这在 文本表示 中非常重要，因为文本的语义通常与其在向量空间中的方向有关。
  2. 余弦相似度通过归一化处理，使得 不同长度 的文本向量可以公平地比较，这对于 文本生成 任务特别有用。
  3. 余弦相似度对文本表示的缩放不敏感，这使得它在处理 不同长度 或不同重要性的文本特征时更加鲁棒。

适用场景

在刚才的讲解中，我专门加粗提示了三个词——文本表示、不同长度和文本生成。

你是否还记得 第15节课 我们提到，除了可以对一个事物（单词或词组）进行嵌入之外，我们还可以对一句话甚至一段话进行嵌入。

对一句话或一段话进行嵌入得到的向量，其实就是文本表示。而当我们比较两句话甚至两段话的时候，显而易见，很多时候，这两句话甚至这两段话的长度是不同的。

因为所有RAG场景，都是以文本生成为最终目标的。所以我们分析了这么多计算距离的方法之后，不难发现，余弦相似度十分适合RAG。

具体实现

余弦距离在向量数据库pgvector里对应的运算符是 <=>。

以下是使用余弦距离计算示例中其他事物与“老婆饼”相似度的代码。

SELECT 1-(向量编码 <=> (SELECT 向量编码 FROM 事物 where name='老婆饼')) AS 距离 FROM 事物;

注意，与前面的L1距离和L2距离相比，我们需要用1减去运算符计算出的结果。

余弦距离在LangChain里面的实现是这样的：

from langchain.evaluation import EmbeddingDistance, load_evaluator

# 加载 embedding_distance 评估器，并指定使用余弦距离
evaluator = load_evaluator("embedding_distance", distance=EmbeddingDistance.COSINE)

# 评估两个字符串的语义相似度
evaluator.evaluate_strings(prediction="I shall go", reference="I will go")

最终选择

现在我们学习了四种相似度计算算法。但是在我们的课程中，我们只能使用一种。那么使用哪一种比较好呢？

结合上面四种算法的适用场景，显而易见，余弦距离是最适合RAG。

至于具体实现，在我们的课程中将使用pgvector。因为在数据检索的探索阶段，使用数据库的配套工具（即上一节课提到的pgadmin），明显比使用LangChain的相似度检索功能更方便。

前面列出LangChain只是因为Langchain是目前最火的RAG相关库，很多现有项目都使用了它。所以万一同学们需要去接手或参与现有RAG项目的时候，很可能只能用LangChain了。

小结

好了，今天这一讲到这里就结束了，最后我们来回顾一下。这一讲我们学会了四种计算两个向量之间距离的方法。

第一种方法是L1距离（曼哈顿距离），是两个点在标准坐标系上的绝对轴距总和。

第二种方法是L2距离（欧几里得距离），是最常见的距离度量方式，也就是两点之间的直线距离。

第三种方法是负内积。

第四种方法是余弦距离，通过计算两个向量的余弦相似度来衡量它们之间的差异。

这种四种方法里面，余弦距离最适合RAG。

思考题

计算两个向量之间距离其实不止以上四种方法，但是为什么只列出以上四种呢？

欢迎你在留言区和我交流互动，如果这节课对你有启发，也推荐分享给身边更多朋友。