03 哈希检索:如何根据用户ID快速查询用户信息?
你好,我是陈东。
在实际应用中,我们经常会面临需要根据键(Key)来查询数据的问题。比如说,给你一个用户ID,要求你查出该用户的具体信息。这样的需求我们应该如何实现呢?你可能会想到,使用有序数组和二叉检索树都可以来实现。具体来说,我们可以将用户ID和用户信息作为一个整体的元素,然后以用户ID作为Key来排序,存入有序数组或者二叉检索树中,这样我们就能通过二分查找算法快速查询到用户信息了。
但是,不管是有序数组、二叉检索树还是跳表,它们的检索效率都是O(log n)。那有没有更高效的检索方案呢?也就是说,有没有能实现O(1)级别的查询方案呢?今天,我们就一起来探讨一下这个问题。
使用Hash函数将Key转换为数组下标
在第1讲中我们说过,数组具有随机访问的特性。那给定一个用户ID,想要查询对应的用户信息,我们能否利用数组的随机访问特性来实现呢?
我们先来看一个例子。假设系统中的用户ID是从1开始的整数,并且随着注册数的增加而增加。如果系统中的用户数是有限的,不会大于10万。那么用户的ID范围就会被固定在1到10万之间。在数字范围有限的情况下,我们完全可以申请一个长度为10万的数组,然后将用户ID作为数组下标,从而实现O(1)级别的查询能力。

将用户ID直接作为下标查询 ,由于数组下标从0开始,因此查询时ID要减1
注意,刚才我们举的这个例子中有一个假设:用户的ID是一个数字,并且范围有限。符合这种假设的用户ID才能作为数组下标,使用数组的随机访问特性,达到O(1)时间代价的高效检索能力。那如果用户的ID数字范围很大,数组无法申请这么大的空间该怎么办呢?或者,用户的ID不是数字而是字符串,还能作为数组下标吗?
我们假设有一个系统使用字符串作为用户ID。如果有一个用户的ID是“tom”,我们该怎么处理呢?我们能否将它转换为一个数字来表示呢?你可以先想一想解决方案,再和我继续往下分析。
我们来考虑这样一种方案:字母表是有限的,只有26个,我们可以用字母在字母表中的位置顺序作为数值。于是,就有:“t” = 20,“o” = 15,“m” = 13。我们可以把这个ID看作是26进制的数字,那么对于“tom”这个字符串,把它转为对应的数值就是20 * 26^2 + 15*26 + 13 =149123,这是一个小于26^4 = 456976的数。
如果所有用户的ID都不超过3个字符,使用这个方法,我们用一个可以存储456976个元素的数组就可以存储所有用户的信息了。实际上,工业界有许多更复杂的将字符串转为整数的哈希算法,但核心思想都是利用每个字符的编码和位置信息进行计算,这里我就不展开了。
那如果内存空间有限,我们只能开辟一个存储10000个元素的数组该怎么办呢?这个时候,我们可以使用“tom”对应的数值149123除以数组长度10000,得到余数9123,用这个余数作为数组下标。
这种将对象转为有限范围的正整数的表示方法,就叫作Hash,翻译过来叫散列,也可以直接音译为哈希。而我们常说的Hash函数就是指具体转换方法的函数。我们将对象进行Hash,用得到的Hash值作为数组下标,将对应元素存在数组中。这个数组就叫作哈希表。这样我们就可以利用数组的随机访问特性,达到O(1)级别的查询性能。
说到这里,你可能会有疑问了,Hash函数真的这么神奇吗?如果两个对象的哈希值是相同的怎么办?事实上,任何Hash函数都有可能造成对象不同,但Hash值相同的冲突。而且,数组空间是有限的,只要被Hash的元素个数大于数组上限,就一定会产生冲突。
对于哈希冲突这个问题,我们有两类解决方案: 一类是构造尽可能理想的Hash函数,使得Hash以后得到的数值尽可能平均分布,从而减少冲突发生的概率;另一类是在冲突发生以后,通过“提供冲突解决方案”来完成存储和查找。最常用的两种冲突解决方案是“开放寻址法”和“链表法”。下面,我就来介绍一下这两种方法,并且重点看看它们对检索效率的影响。
如何利用开放寻址法解决Hash冲突?
所谓“开放寻址法”,就是在冲突发生以后,最新的元素需要寻找新空闲的数组位置完成插入。那我们该如何寻找新空闲的位置呢?我们可以使用一种叫作“线性探查”(Linear Probing)的方案来进行查找。
“线性探查”的插入逻辑很简单:在当前位置发现有冲突以后,就顺序去查看数组的下一个位置,看看是否空闲。如果有空闲,就插入;如果不是空闲,再顺序去看下一个位置,直到找到空闲位置插入为止。
查询逻辑也和插入逻辑相似。我们先根据Hash值去查找相应数组下标的元素,如果该位置不为空,但是存储元素的Key和查询的Key不一致,那就顺序到数组下一个位置去检索,就这样依次比较Key。如果访问元素的Key和查询Key相等,我们就在哈希表中找到了对应元素;如果遍历到空闲处,依然没有元素的Key和查询Key相等,则说明哈希表中不存在该元素。
为了帮助你更好地理解,我们来看一个例子。
假设一个哈希表中已经插入了两个Key,key1和key2。其中Hash(key1) = 1, Hash(key2) = 2。这时,如果我们要插入一个Hash值为1的key3。根据线性探查的插入逻辑,通过3步,我们就可以将key3插入到哈希表下标为3的位置中。插入的过程如下:
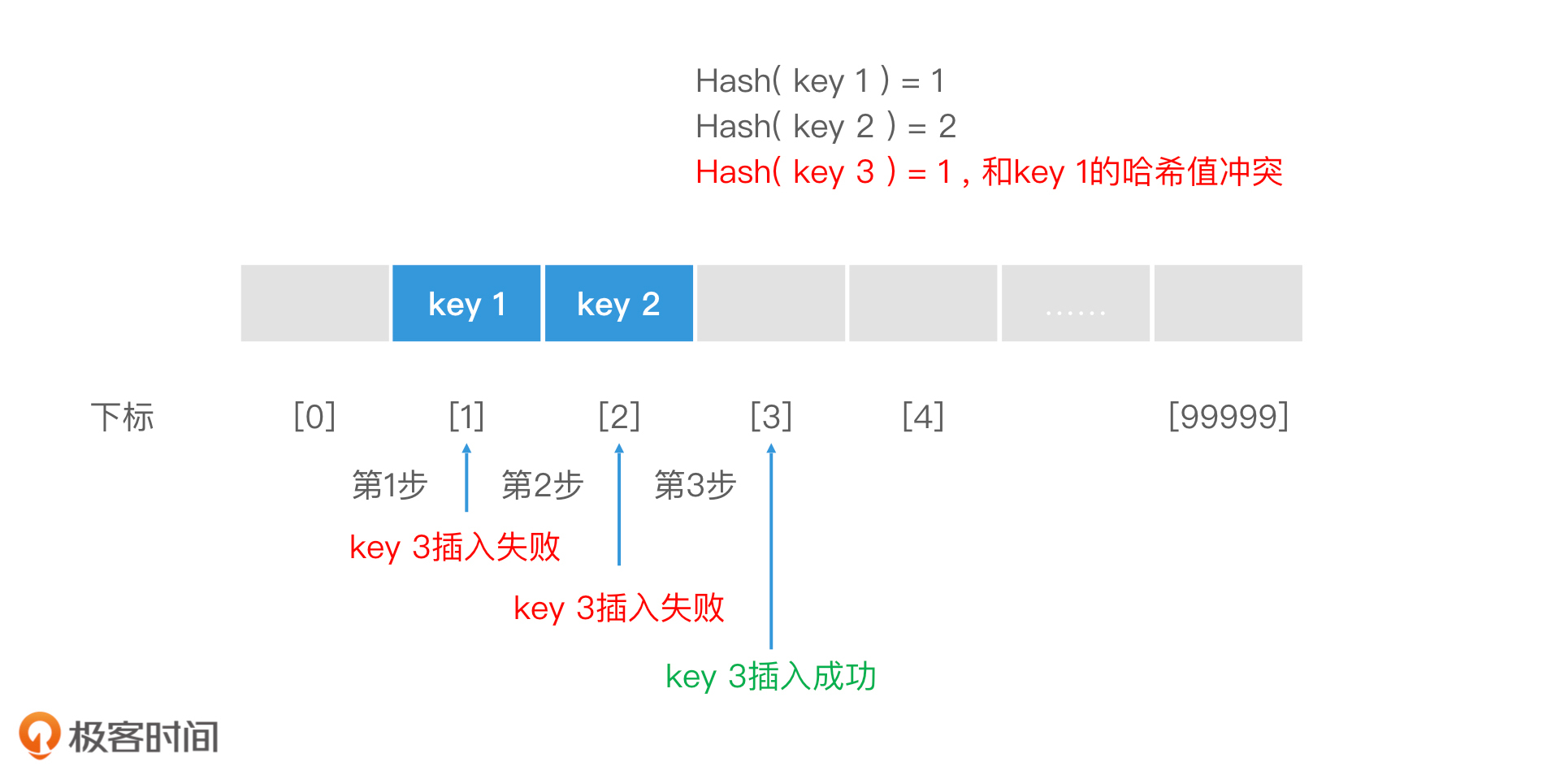
在查找key3的时候,因为Hash(key3)= 1,我们会从哈希表下标为1的位置开始顺序查找,经过3步找到key3,查询结束。
讲到这里,你可能已经发现了一个问题:当我们插入一个Key时,如果哈希表已经比较满了,这个Key就会沿着数组一直顺序遍历,直到遇到空位置才会成功插入。查询的时候也一样。但是,顺序遍历的代价是O(n),这样的检索性能很差。
更糟糕的是,如果我们在插入key1后,先插入key3再插入key2,那key3就会抢占key2的位置,影响key2的插入和查询效率。因此,“线性探查”会影响哈希表的整体性能,而不只是Hash值冲突的Key。
为了解决这个问题,我们可以使用“二次探查”(Quadratic Probing)和“双散列”(Double Hash)这两个方法进行优化。下面,我来分别解释一下这两个方法的优化原理。
二次探查就是将线性探查的步长从i改为i^2:第一次探查,位置为Hash(key) + 1^2;第二次探查,位置为Hash(key) +2^2;第三次探查,位置为Hash(key) + 3^2,依此类推。
双散列就是使用多个Hash函数来求下标位置,当第一个Hash函数求出来的位置冲突时,启用第二个Hash函数,算出第二次探查的位置;如果还冲突,则启用第三个Hash函数,算出第三次探查的位置,依此类推。
无论是二次探查还是双散列,核心思路其实都是在发生冲突的情况下,将下个位置尽可能地岔开,让数据尽可能地随机分散存储,来降低对不相干Key的干扰,从而提高整体的检索效率。
但是,对于开放寻址法来说,无论使用什么优化方案,随着插入的元素越多、哈希表越满,插入和检索的性能也就下降得越厉害。在极端情况下,当哈希表被写满的时候,为了保证能插入新元素,我们只能重新生成一个更大的哈希表,将旧哈希表中的所有数据重新Hash一次写入新的哈希表,也就是Re-Hash,这样会造成非常大的额外开销。因此,在数据动态变化的场景下,使用开放寻址法并不是最合适的方案。
如何利用链表法解决Hash冲突?
相比开放寻址法,还有一种更常见的冲突解决方案,链表法。所谓“链表法”,就是在数组中不存储一个具体元素,而是存储一个链表头。如果一个Key经过Hash函数计算,得到了对应的数组下标,那么我们就将它加入该位置所存的链表的尾部。
这样做的好处是,如果key3和key1发生了冲突,那么key3会通过链表的方式链接在key1的后面,而不是去占据key2的位置。这样当key2插入时,就不会有冲突了。最终效果如下图。
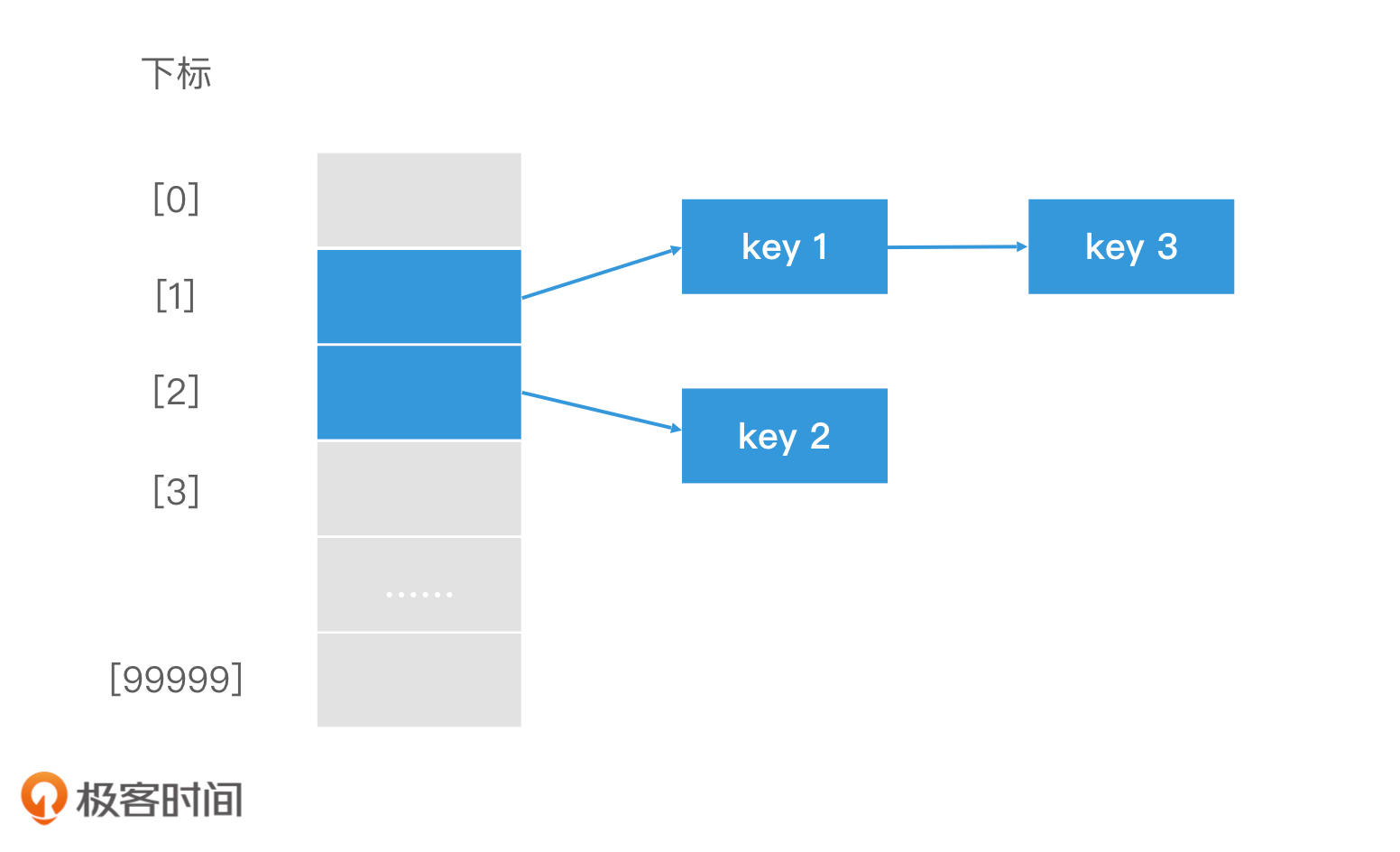
链表法
讲到这里,你可能已经发现了,其实链表法就是将我们前面讲过的数组和链表进行结合,既利用了数组的随机访问特性,又利用了链表的动态修改特性,同时提供了快速查询和动态修改的能力。
想要查询时,我们会先根据查询Key的Hash值,去查找相应数组下标的链表。如果链表为空,则表示不存在该元素;如果链表不为空,则遍历链表,直到找到Key相等的对应元素为止。
但是,如果链表很长,遍历代价还是会很高。那我们有没有更好的检索方案呢?你可以回想一下,在上一讲中我们就是用二叉检索树或跳表代替链表,来提高检索效率的。
实际上,在JDK1.8 之后,Java中HashMap的实现就是在链表到了一定的长度时,将它转为红黑树;而当红黑树中的节点低于一定阈值时,就将它退化为链表。
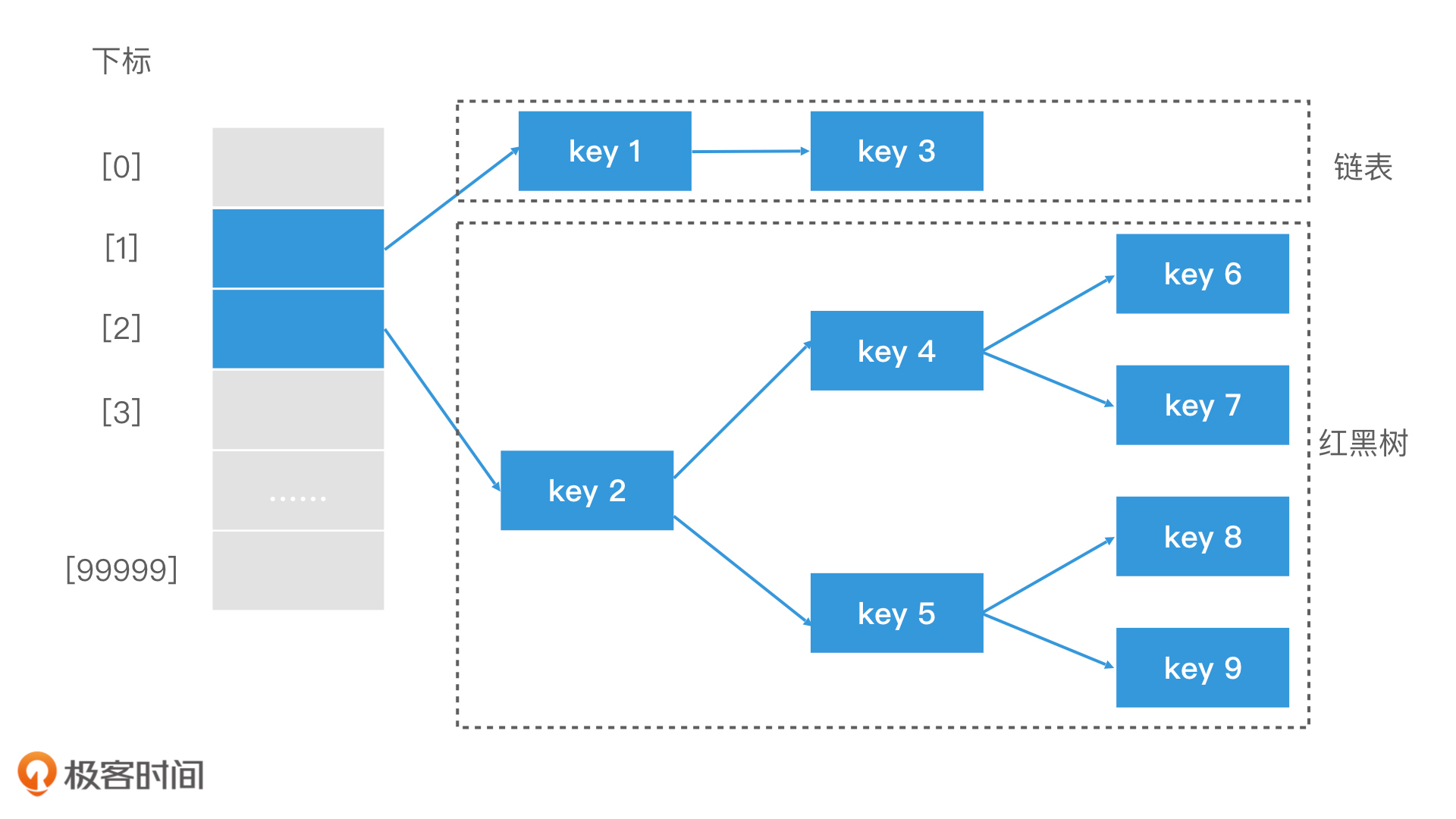
链表法:用红黑树来优化长链表
第一个阶段,通过Hash函数将要查询的Key转为数组下标,去查询对应的位置。这个阶段的查询代价是O(1)级别。
第二阶段,将数组下标所存的链表头或树根取出。如果是链表,就使用遍历的方式查找,这部分查询的时间代价是O(n)。由于链表长度是有上限的,因此实际开销并不会很大,可以视为常数级别时间。如果是红黑树,则用二分查找的方式去查询,时间代价是O(log n)。如果哈希表中冲突的元素不多,那么落入红黑树的数据规模也不会太大,红黑树中的检索代价也可以视为常数级别时间。
哈希表有什么缺点?
哈希表既有接近O(1)的检索效率,又能支持动态数据的场景,看起来非常好,那是不是在任何场景下,我们都可以用它来代替有序数组和二叉检索树呢?答案是否定的。前面我们说了这么多哈希表的优点,下面我们就来讲讲它的缺点。
首先,哈希表接近O(1)的检索效率是有前提条件的,就是哈希表要足够大和有足够的空闲位置,否则就会非常容易发生冲突。我们一般用装载因子(load factor)来表示哈希表的填充率。装载因子 = 哈希表中元素个数/哈希表的长度。
如果频繁发生冲突,大部分的数据会被持续地添加到链表或二叉检索树中,检索也会发生在链表或者二叉检索树中,这样检索效率就会退化。因此,为了保证哈希表的检索效率,我们需要预估哈希表中的数据量,提前生成足够大的哈希表。按经验来说,我们一般要预留一半以上的空闲位置,哈希表才会有足够优秀的检索效率。这就让哈希表和有序数组、二叉检索树相比,需要的存储空间更多了。
另一方面,尽管哈希表使用Hash值直接进行下标访问,带来了O(1)级别的查询能力,但是也失去了“有序存储”这个特点。因此,如果我们的查询场景需要遍历数据,或者需要进行范围查询,那么哈希表本身是没有什么加速办法的。比如说,如果我们在一个很大的哈希表中存储了少数的几个元素,为了知道存储了哪些元素,我们只能从哈希表的第一个位置开始遍历,直到结尾,这样性能并不好。
重点回顾
好了,关于哈希检索我们就讲到这里。你会看到,哈希表的本质是一个数组,它通过Hash函数将查询的Key转为数组下标,利用数组的随机访问特性,使得我们能在O(1)的时间代价内完成检索。
尽管哈希检索没有使用二分查找,但无论是设计理想的哈希函数,还是保证哈希表有足够的空闲位置,包括解决冲突的“二次探查”和“双散列”方案,本质上都是希望数据插入哈希表的时候,分布能均衡,这样检索才能更高效。从这个角度来看,其实哈希检索提高检索效率的原理,和二叉检索树需要平衡左右子树深度的原理是一样的,也就是说,高效的检索需要均匀划分检索空间。
另一方面,你会看到,复杂的数据结构和检索算法其实都是由最基础的数据结构和算法组成的。比如说JDK1.8中哈希表的实现,就是使用了数组、链表、红黑树这三种数据结构和相应的检索算法。因此,对于这些基础的数据结构,我们需要深刻地理解它们的检索原理和适用场景,这也为我们未来学习更复杂的系统打下了扎实的基础。
课堂讨论
假设一个哈希表是使用开放寻址法实现的,如果我们需要删除其中一个元素,可以直接删除吗?为什么呢?如果这个哈希表是使用链表法实现的会有不同吗?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这篇文章分享给你的朋友。
- 徐洲更 👍(23) 💬(3)
我这几天刚好看过一个C语言的哈希表实现源代码khash.h,它用的就是open addressing方法。 在删除元素的时候 不会真正的删除,会有一个flag记录状态。后续插入新的元素还能用。否则就会导致每次就要重新申请内存,rehash,计算量太大。链表法的话,删除的是对应的node ,时间复杂度是O(1) 所以删除很快
2020-03-28 - 每天晒白牙 👍(11) 💬(2)
链表法可以直接删除,开放寻址法不行。 开放寻址法在 hash 冲突后会继续往后面看,如果为空,就放到后面,这样会存在连续的几个值的 hash 值都相同的情况,但如果想删除的数据在中间的话,就会影响对后面数据的查询了 可以增加一个删除标识,这种添加删除标识的在数据库中也常用
2020-03-28 - 奕 👍(8) 💬(1)
通过开放寻址法是不可以简单的删除元素的,如果要删除的元素是通过寻址法找的存储下标,那么该元素所在的下标不是本身 hash 后的位置 链表法是可以的:因为元素本身的 hash 值和存储位置的下标 值是一致的
2020-03-27 - pedro 👍(6) 💬(3)
今天的内容权当回顾吧,期待后续的干货。
2020-03-27 - Bachue Zhou 👍(5) 💬(1)
感觉当使用链表法时,哈希算法就不再是完整的搜索算法了,而只是为下一步搜索算法减少搜索范围的算法,至于下一步算法是什么,其实没啥限制,既可以是链表或平衡树,也可以是另一个哈希算法。
2020-12-18 - 研发 👍(4) 💬(2)
为什么哈希表没有有序存储的能力? 有序存储指的不是存入和取出元素的顺序是一致的吗?哈希表本质是数组,数组是有序存储的,为什么哈希表不是?
2020-06-26 - yang 👍(3) 💬(1)
看了一下评论区和老师的回复,先回答问题: 1. 链表法删除元素: 用Hash(Key)找到对应的下标,根据下标在数组找到了这个节点 node = table[index],那删除就可以直接 node = node.next;这里数组里存的不是虚头节点呀,是真实的元素呀? 2. 开放寻址法中的 线性探测、二次线性探测、双散列也好,都是在得到的index 对应的table[index] != null 的情况下,以不同形式继续找, 那我想问一下老师,这里table[index] != null 的时候,会比较 已存在元素 和 待插入元素的 key 吗? 也就是说, 开放寻址法是否允许key相同的元素存在呢? 因为我看文章,在开放寻址法中,只是判断 计算出来位置对应的元素是否存在,并没有比较存在时,两者的key是否相同。 如果允许元素的key相同,这样会影响删除方式。 如果允许key相同的元素存在,删除的时候应该用同样的开放寻址法找到最后一个不为空 且key相同的元素置为null。 如果不允许key相同的元素存在,那就像老师给其他同学评论的,a b c计算出的hash值相同,位置连续, 删除b,会出现空洞的情况,影响这一局部元素的插入 删除 查询。老师给出的方法是:增加标记位,删除为true, 查询、删除遇到删除=true的情况可以继续往后找,新增元素 遇到 删除=true的时候可以直接替换,并修改状态为false; 疑问: a. 不管是 线性探测法、二次探测法、双散列,只要到了数组最后一个元素发现是满的时候,就会扩容 产生rehash吗? b. 不论是 线性探测法、二次探测法、双散列,他们在插入元素的时候,会比较已存在元素和待插入元素的key是否相同吗?也就是说允许key重复的元素出现吗? c. 线性探测法步长为1,二次探测法采用index = index + 2^i (i为第几次探测)进行探测、 我想问的是双散列,第一次通过Hash(Key)得到的index位置上有元素,那么第二次的Hash函数是不是就是上一次用到的Hash函数呢? 另外,每次Hash的时候,其中的key是怎么变的啊? 字有点多,恳请老师见谅~!
2020-04-09 - aoe 👍(3) 💬(1)
原来处理冲突还可以用“开放寻址”的方法!又学习了通过flag标记可以解决删除问题。强大的flag,环形数组也用了这个标记,让实现变简单了,还给flag起了个拉风的名字“哨兵”
2020-04-02 - 阿斯蒂芬 👍(2) 💬(1)
哈希(散列)算得上是基础常用的top3数据结构了吧。 写几点感悟: 一:散列函数的耗时为什么被「忽略」? 之前在阅读《算法图解》中,散列表有一段这样的描述: 「你结合使用散列函数和数组创建了一种被称为散列表(hashtable)的数据结构。散列表是你学习的第一种包含额外逻辑的数据结构」 我觉得这个「包含额外逻辑」从一个特别的角度描述了散列表的特性。比起数组和链表家族,散列表的存取阶段都多了一步「计算散列(哈希)值并映射」的过程,其实这个就是额外的逻辑。然而经常在讨论散列表的性能时,通常会「达成共识忽略」这一步的性能和具体实现细节。其实为什么呢? 尝试理解下:就如老师举例说明的使用英文字母序号做系数再加上二十六进制指数的「魔法」一样,散列值的本质就是「计算」,而恰恰现代计算机最强的功能之一就是计算,感谢数学家和计算机科学家的努力,发明高效且分布均匀的散列函数,可以说几乎对大多数程序员的大多数场景下都是透明的,我们可以接近将这一步骤当作常数级别的耗时,因此在分析散列表的总耗时的时候,可以愉快地忽略,而只需要关注真正用于检索的耗时,比如定位到了索引后可能需要的内存交互甚至磁盘交互的耗时。 二:开放寻址法如此「不堪」,有什么应用场景? 虽然讲到散列冲突的解决方案,开放寻址法总是第一个拿出来被「锤」,但是既然天天被吊打,为什么还要学,实际有什么用处?这里又到了应用「实际场景」的思维模型了。Java的ThreadLocal用来存储线程隔离的本地变量,其中有个ThreadLocalMap散列结构,内部解决散列冲突的策略就是开放寻址法。为什么它会这么淡定使用呢,个人理解还是因为它的使用场景相对简单,一般往ThreadLocal中存放的数据量不大,使用开放寻址而不是链表法,节省了链表的指针开销,而且兼顾了效率,ThreadLocalMap的场景非常契合开放寻址的优点。 以上两点感悟还处于自我总结阶段,没有很多查证,还望老师指点。
2020-04-12 - 峰 👍(2) 💬(1)
不能,这样不能和数据不存在的情况区分,链表法就可以了,核心考量是冲突元素是否是聚集的。 hash 表中的hash 是一个将key 转化成数组下标的映射关系,我们这里只讲到这个转化尽可能的均匀的散列,但如果加上尽可能保留原始key 空间的距离大小信息(以前我学降维得出的结论是数据降维要做的事情是把你想从高维空间保留的信息尽可能在数据的低维表示上同样成立),是否就可以在一定程度上解决hash 完全没法做范围查询的缺陷,好早之前看过点局部敏感hash 的一些东东,想来应该可以结合。
2020-03-27 - 柏油 👍(1) 💬(1)
开放寻址法从理论上讲应该也是可以删除的,不过稍微麻烦些,需要保证同一hash值删除的key前后元素串联性,以保证此hash值在删除当前key之后的元素能被寻址到,可以用特殊值代替,但是在检索时可能会遍历这些特殊值 效率上更低;而链表法则可以很好的支持删除
2020-03-27 - benny 👍(0) 💬(1)
就是哈希表要足够大和有足够的空闲位置 这里空间大也是为了进行hash计算时可以更好的散列吧?
2021-05-01 - 森林木 👍(0) 💬(1)
如果使用开放寻址法,不能直接删除否则会影响后面的检索;如果是链表法则无所谓
2021-04-07 - 一粒 👍(0) 💬(1)
数组(哈希表)的大小不能被改变,否则该位置之后存储的元素就找不到了。这和分布式系统中数据分片不能被改变的道理一样。 所以,当装载因子过大,需要更换更大的数组时,已存元素的哈希值都要被重新计算才行。
2021-01-24 - 明翼 👍(0) 💬(1)
hash表如何持久化,特别是拉链方式的哈希表的持久化,老师可以给个思路吗?
2020-11-25