25 可靠性基础科学：可靠性背后的运筹学和概率学

你好，我是白园。今天我们聊一下可靠性背后的一些基础学科——运筹学和概率学的知识。

概率学

首先看下概率学相关的，在添加监控和报警的时候，我们发现服务A同时对外提供了多个功能，比如点赞、评论、互动等都是服务A同时提供的。同时还带了几十个小的功能，这个时候如果我们想配置可用性的报警，是都配置还是只配置几个重要的就行呢？其实这个背后就会涉及到一个概率学的知识。

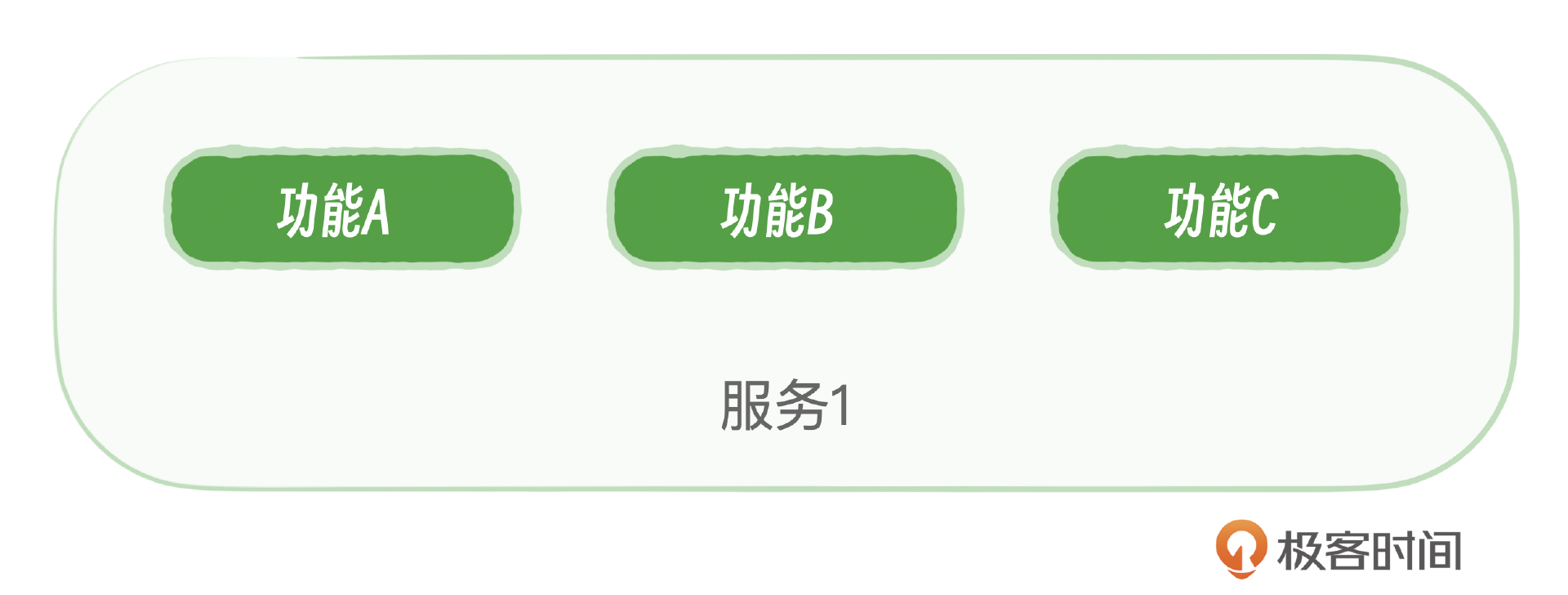
就是当A1发生的时候，B1同时发生的概率是多少。如果A1发生的时候，B1也同时概率超过99%。这个时候只需要保证A1的可用性就行；如果A1发生的时候，B1同时概率很低，那这个时候就必须添加B1报警。这背后其实就是一个概率学上的分析，是否是独立事件的分析。

当A1发生时，B1同时发生的概率可以通过条件概率来计算，公式如下：

$$P(B1|A1)=\frac{P(A1\cap B1)}{P(A1)}$$

这里：

$P(B1|A1)$ 是在A1发生故障的时候B1发生故障的概率；
$P(A1\cap B1)$ 是A1与B1同时发生的概率；
$P(A1)$ 是A1发生的概率。

如果A1发生时，B1同时发生的概率超过某个阈值，比如99%，即 $[P(B1|A1) > 0.99]$ 这意味着在A1发生的情况下，B1发生的可能性非常高，可以保证召回率大于99%。在这种情况下，确保A1的可用性可能就足够了，因为B1的发生几乎可以被预测。

然而，如果A1发生时，B1同时发生的概率很低 $[P(B1|A1) \ll 0.99]$，那么需要对B1也添加报警机制，避免可能的风险或损失。

这个时候就需要从部署的情况来看了，如果服务1同时提供A、B两个功能，对于可用性来说，功能A、B往往是同时出现问题；因为服务是部署在一起的，就不是独立事件。如果做了微服务，功能A由服务1提供；功能B由功能2提供。这个时候就是A、B就是一个相互独立事件。

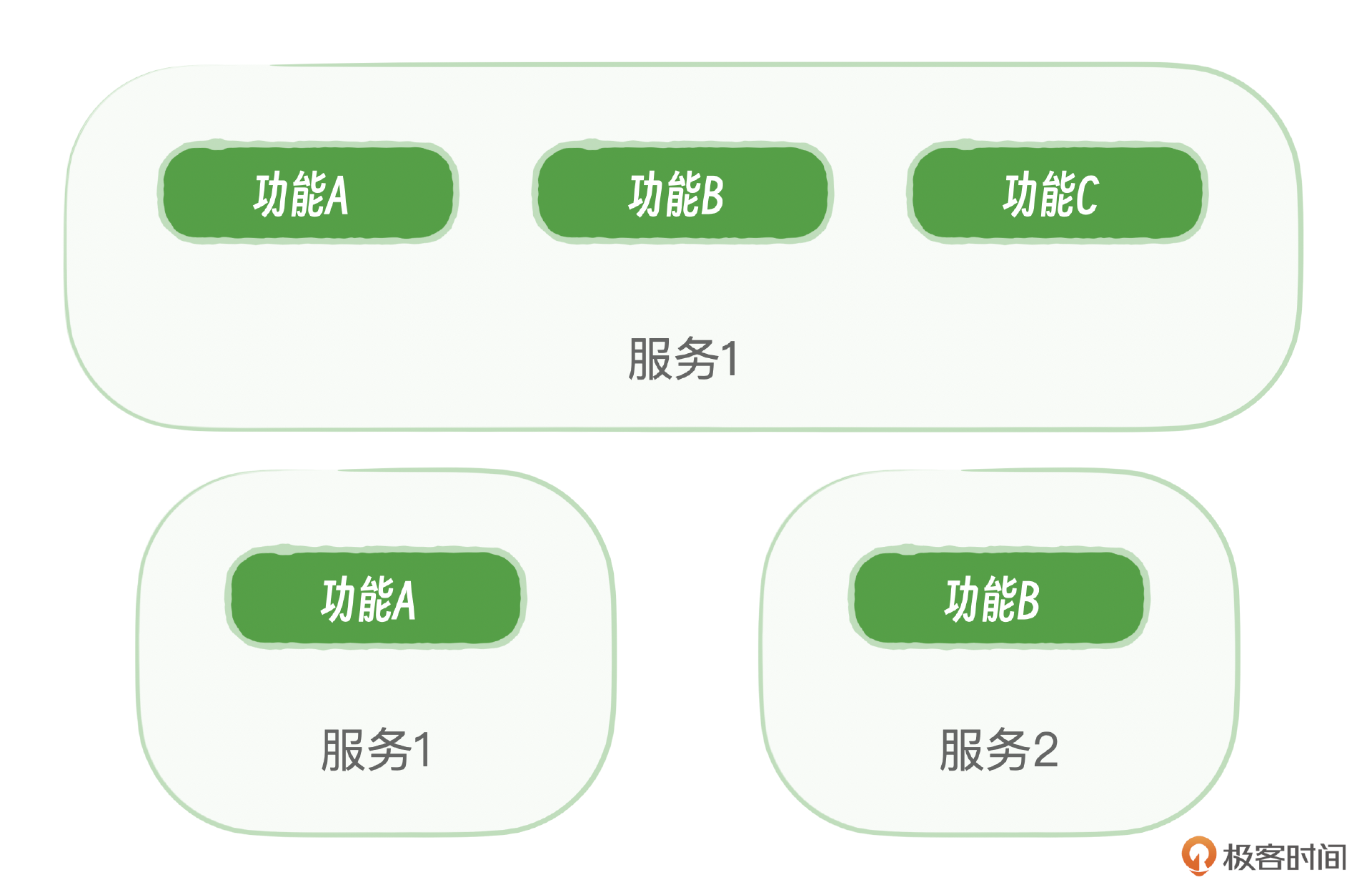
因为在部署服务时，服务1同时提供功能A和功能B，如果这两个功能是部署在一起的，它们可能共享相同的硬件、网络或软件环境，因此它们发生故障可能是相互关联的。在这种情况下，功能A和功能B不是独立事件，它们发生故障的概率不是通过简单的乘法规则来计算的。

当服务1和2被拆分成微服务架构，功能A由服务1提供，功能B由服务2提供，如果它们在不同的硬件、网络或软件环境中运行，那么它们发生故障的概率可以认为是独立的。

微服务架构的优势之一就是它允许服务组件独立运行和扩展，减少了单点故障的风险。如果服务1和2是完全独立的，那么一个服务的故障不太可能影响另一个服务，从而提高了整个系统的可用性和容错性。但是如果服务拆分的过细就容易陷入另外一个极端，服务数量膨胀，资源无法充分的利用。

在进行报警和监控系统的优化与整合时，应采用概率学视角来评估报警设置的必要性。具体而言，需要分析并判断是否每一类报警都确实需要被纳入监控体系，就可以从更多的视角来看待问题。

运筹学

在可靠性保证的工作中往往会面对很多突发状况，往往需要团队成员共同讨论和作出决策。由于缺乏明确的责任归属，决策过程中常出现犹豫不决的现象。

决策瓶颈往往源于缺乏一套坚实的理论支撑。如果我们能够依据一套科学的理论模型来指导决策，那么整个过程将变得更加客观和系统化。这种方法不仅能显著提高决策效率，还能在事后评估时，避免将责任不公正地归咎于任何个人。

这背后的理论支撑就是运筹学里面的决策论。决策的情况分两种，一种是概率不确定的风险如何决策，一种是概率明确的风险如何决策。

概率不明确风险的如何决策？

我曾经遇到过一个紧急案例，机房突然接到市电供应中断的通知，目前只能依靠不太稳定的柴油发电机来维持电力供应。面对这种高风险状况，我们需要迅速做出关键决策：立即将流量迁移到其他机房，或是继续依赖可能发生故障的柴油发电机。

选择立即迁移流量虽然可能导致服务功能因其他机房的容量限制而有所降低，从而带来一些损失，但这一策略可以最大限度地规避潜在的更大风险。而如果选择留在原地不转移，一旦柴油发电机故障，我们将面临长达1～2小时的服务全面中断，这将带来极为严重的后果。

在这种情况下，如何决策呢？又有哪些运筹学的知识呢？在这种情况下，如何做出合理的决策至关重要。定最优策略前面临的主要挑战是柴油发电机故障的概率不明确，这给决策带来了不确定性。在这种情况下，我们可以考虑几种常见的决策原则来指导我们做出选择。

乐观原则：有的人基于对机房可靠性的信心，选择不进行流量转移，坚持当前供电方案。
悲观原则：有的人出于对机房可能发生故障的担忧，立即执行流量转移，以避免潜在的大规模服务中断。
最小后悔原则（最小最大遗憾原则或Savage准则）在不确定性下做出决策，它考虑了在每种情况下可能发生的最坏结果，并试图最小化这种最坏结果的遗憾值。

以下是使用最小后悔原则进行决策的步骤：

确定可能的决策：在这种情况下，我们有两个决策选项，提前将流量切走和不切走，等待柴油发电机的表现。
确定可能的结果：对于每个决策，确定可能发生的结果。例如：
如果切走流量，可能的结果包括其他机房容量不够导致功能降级，柴油发电机正常工作，业务没有受到影响。
如果不切走流量，可能的结果包括柴油发电机正常工作，业务没有受到影响，柴油发电机故障，导致大面积服务不可用。
评估每个结果的遗憾值：对于每个结果，评估其遗憾值或损失。遗憾值是如果结果发生，你会感到多么后悔没有选择另一种决策。
计算每个决策的遗憾值：对于每个决策，计算在所有可能结果下的最大遗憾值。
选择具有最小最大遗憾值的决策：选择那个在最坏情况下遗憾值最小的决策。

应用最小后悔原则之后，我们来看一下简化后的示例结果。

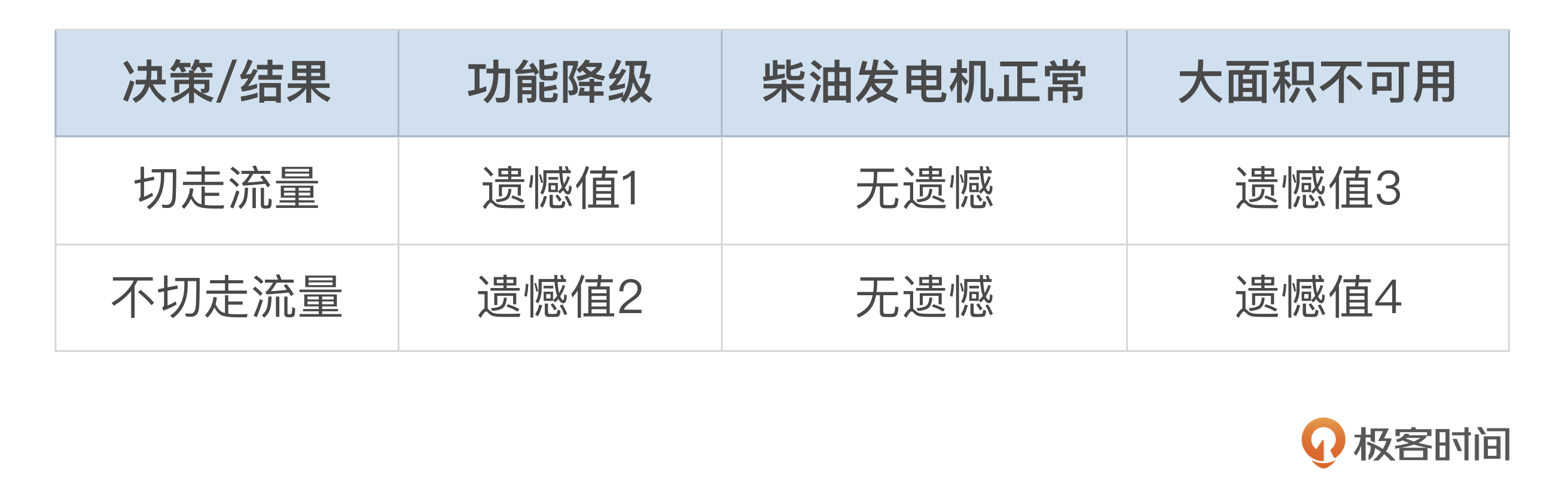
在这个表中，遗憾值1、2、3和4需要根据实际情况进行评估。例如，如果大面积不可用的后果远比功能降级更严重，那么遗憾值4可能会远大于遗憾值1。

根据上表，我们可以进行以下计算：

决策A的最大遗憾值：max(遗憾值1, 遗憾值3)
决策B的最大遗憾值：max(遗憾值2, 遗憾值4)

如果max(遗憾值1, 遗憾值3) < max(遗憾值2, 遗憾值4)，则选择决策A（提前切走流量）。反之，则选择决策B。

当你需要给老板决策的时候，你就可以利用运筹学的知识提供多个原则供老板去参考和决策，需要让老板在乐观、悲观、最小最大后悔原则直接做出判断和决策。

概率明确如何决策？

如果这个柴发确定停止发电了，这个时候就是变成了概率明确的故障， 针对概率明确故障 这里采用的是贝叶斯原则，也就是收益最大化的原则；根据不同的机房和故障情况，给出当前损失最小的预案。

这个时候我们就可能面临多个条件，容量有限的情况如何保障最核心的业务，让损失最小。这里我们采用线性规划来实现。当考虑到部分运行业务时，线性规划模型需要进行相应的调整，因为决策变量不再局限于0或1（完全不运行或完全运行），而是可以取0到1之间的任何值，表示业务运行的程度。以下是调整后的步骤：

定义目标函数：目标是最小化业务损失，可以通过最大化关键业务的部分或全部运行来实现。
确定决策变量：为每个业务定义决策变量，表示该业务的运行程度。
$$x_{i}$$：第i个业务的运行程度（0表示完全不运行，1表示完全运行）
建立约束条件
容量约束：所有业务运行所需的资源总和不能超过机房的容量限制。

$( \sum_{i=1}^{n} a_{i} x_i \leq C )$，其中 $( a_{i} )$ 是第i个业务在 $( x_i )$ 运行程度下所需的资源量，$( C )$ 是机房的容量限制。

业务依赖性约束：确保依赖于其他业务的业务至少运行到一定程度。
最小运行约束：对于关键业务，可能需要设置最小运行程度的要求。
量化业务价值：为每个业务分配一个权重，表示其对整体业务的重要性。
$( w_i )$：第 ( i ) 个业务的权重。
构建线性规划模型
目标函数：最大化总权重与运行程度的乘积
$( \max \sum_{i=1}^{n} w_i x_i )$
约束条件：包括容量约束、业务依赖性约束和最小运行约束。
求解线性规划问题：使用适当的线性规划求解器求解上述问题。
实施解决方案：根据求解结果，调整各业务的运行程度。

你可以看一下使用Python的 scipy.optimize 模块进行线性规划的示例代码。

from scipy.optimize import linprog

# 业务权重
weights = [20, 15, 10, 5]  # 假设有4个业务，不同的权重

# 每个业务在完全运行时所需的资源量
full_resource_requirements = [100, 80, 60, 40]

# 机房容量限制
capacity = 250

# 目标函数系数（我们希望最大化这个值）
c = weights

# 约束条件的不等式系数矩阵
A_ub = [[-1] * len(full_resource_requirements)]  # 资源限制
b_ub = [-capacity]  # 容量限制

# 每个业务的资源需求与其运行程度的乘积
resource_requirements = [frr / 100 * i for frr in full_resource_requirements for i in range(101)]

# 更新约束条件
A_ub += [[req if j == i else 0 for j in range(len(resource_requirements))]
         for i, req in enumerate(resource_requirements)]

# 决策变量的界限（0表示不运行，100表示完全运行）
x_bounds = [(0, 100) for _ in range(len(resource_requirements))]

# 使用单纯形算法求解线性规划问题
res = linprog(c=c, A_ub=A_ub, b_ub=b_ub, bounds=x_bounds, method='highs')

# 将结果转换为每个业务的运行程度
business_operation_levels = [res.x[i:i+100] for i in range(0, len(res.x), 100)]

# 输出结果
print(f"每个业务的运行程度：{business_operation_levels}")
print(f"最大化权重总和：{-res.fun}")

请注意，这个示例代码是一个简化的版本，实际应用中需要根据具体情况定义权重、资源需求和约束条件。此外，当业务可以部分运行时，可能需要更精细的资源分配策略，以及更复杂的模型来反映不同运行程度下的资源消耗和业务价值。小。

小结

这节课我简单介绍了一下可靠性其背后蕴含的大量概率学、运筹学等知识，希望可以帮助你在日常问题中做出不同角度的思考。可靠性背后还有很多其他的知识我就不一一分享了，需要你去探索，这里我分享一些好的课程给你，周志华老师的机器学习、王焕钢老师的运筹学、保罗.罗基的可靠性科学，如果你感兴趣的话，可以自己去读一读。

思考题

你平时还有哪些跟可靠性跟基础学科的思路和场景，欢迎分享到评论区，也欢迎你把这节课的内容分享给其他朋友。