21 AIOps容量预测:如何准确地预估流量?
你好,我是白园。
从今天我们进入AIOps的容量部分,来看AI跟容量结合能产生哪些火花。容量本质上是资源消耗与资源补充之间的平衡。我们的目标是在确保系统可靠性的同时,尽可能地减少资源的使用。
这其中涉及了容量的三个要素:流量波动、资源供给、资源分配。这节课我们就从这三点出发,看看如何准确预测流量、如何合理预估资源、如何分配资源让收益最大化。

流量预测
流量受多种因素影响,其中最主要的是3点:一是用户习惯,不同产品形态吸引的用户行为模式各异。例如,打车软件需关注早晚高峰时段,短视频是在晚饭后迎来流量高峰,而办公软件的流量峰值通常出现在工作时间点。二是工作日与周末差异,周末用户在家或外出的时间增多,这会导致流量模式与工作日相比出现变化。三是节假日及重大事件,比如国庆、元旦、春节,以及重大体育赛事等,都会对流量产生显著影响。
那么怎么预测流量的波动呢?今天我重点介绍一个算法——Holt-Winters。Holt-Winters模型是一种用于时间序列预测的指数平滑方法,可以处理具有趋势和季节性的时间序列数据。Holt-Winters方法有三个主要组成部分:
- 简单指数平滑,预测没有趋势和季节性的数据。
- 线性趋势方法,预测具有线性趋势的数据。
- 季节性方法,预测具有季节性模式的数据。
Holt-Winters季节性方法通过结合趋势和季节性组件来预测未来的值。它使用三个参数:α(平滑系数)、β(趋势平滑系数)和γ(季节性平滑系数),这些参数决定了模型对新数据的响应速度以及对趋势和季节性的调整速度。
预测公式如下:
- $ L_t = \alpha \times (Y_t - S_{t-m}) + (1 - \alpha) \times (L_{t-1} + T_{t-1}) $(水平)
- $T_t = \beta \times (L_t - L_{t-1}) + (1 - \beta) \times T_{t-1}$(趋势)
- $S_t = \gamma \times (Y_t - L_{t-m}) + (1 - \gamma) \times S_{t-m}$(季节性)
其中:
- ( $Y_t$) 是在时间点t的实际观测值。
- ( $L_t$) 是在时间点t的预测水平。
- ( $T_t$) 是在时间点t的预测趋势。
- ( $S_t$) 是在时间点t的季节性因子。
- ( $m$ ) 是季节性周期的长度。
Holt-Winters方法可以用于短期预测,也可以通过调整参数来适应长期预测。它广泛应用于经济、金融、气象和许多其他领域。
同时我们在进行流量预测的时候,还需要纳入节假日和重大活动的潜在影响。基于常规的三次平滑预测方法,我们将进一步叠加节假日效应,来捕捉由特殊事件引发的流量波动。这些影响数据可以基于历史经验预先设定,并录入数据库。
例如,我们可以预见到在1月1日午夜,流量可能会比前10分钟激增300%。因此,在模型训练时,我们会把这一预期增长纳入考量,也就是把前一天23:50的流量数据基础上增加300%,来更准确地预测1月1日0点的流量高峰。
代码demo供你参考:
import pandas as pd
from statsmodels.tsa.holtwinters import ExponentialSmoothing
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
# 假设CSV文件包含日期和流量数据,日期列为'date',流量列为'traffic'
traffic_data = pd.read_csv('traffic_data.csv', parse_dates=['date'], index_col='date')
# 假设节假日数据包含日期和叠加因子,日期列为'date',叠加因子列为'factor'
holidays_data = pd.read_csv('holidays_data.csv')
# 应用节假日叠加因子到流量数据
for index, row in holidays_data.iterrows():
traffic_data.loc[row['date']] *= row['factor']
# 初始化Holt-Winters模型
# 这里的参数trend='add'表示添加趋势组件,seasonal='add'表示添加季节性组件
# seasonal_periods为季节周期,例如每月数据为12
model = ExponentialSmoothing(traffic_data, trend='add', seasonal='add', seasonal_periods=12)
# 拟合模型
model_fit = model.fit()
# 预测未来流量,例如预测接下来12个周期的流量
forecast = model_fit.forecast(12)
# 可视化实际流量和预测流量
plt.figure(figsize=(12, 6))
plt.plot(traffic_data.index, traffic_data, label='Actual Traffic')
plt.plot(forecast.index, forecast, label='Forecast Traffic', color='red')
plt.legend()
plt.title('Traffic Forecast with Holt-Winters Method')
plt.xlabel('Date')
plt.ylabel('Traffic')
plt.show()
# 如果有实际的流量数据用于评估
# actual_traffic = pd.read_csv('actual_traffic.csv', parse_dates=['date'], index_col='date')
# 计算MSE和RMSE
# mse = mean_squared_error(actual_traffic, forecast)
# rmse = np.sqrt(mse)
# print(f'MSE: {mse}, RMSE: {rmse}')
还有 traffic_data.csv 和 holidays_data.csv 文件的示例格式。
traffic_data.csv
holidays_data.csv
时间序列预测模型有许多不同的方法和算法,每种方法都有优势和适用场景。我们看一下常见的时间序列预测模型的对比。
- Holt-Winters:指数平滑方法简单易用,适用于平稳数据,对异常值较为敏感。
- ARIMA:适用于非平稳数据,能够处理趋势和季节性,但需要较多的调参。
- Prophet:Facebook开发的新型模型,能够处理节假日效应和趋势变化。
- LSTM:一种基于神经网络的模型,适用于处理长期依赖关系和非线性关系,但需要更多的数据和计算资源。
资源画像
我们有了流量,那第二步就是解决资源消耗的问题,需要针对不同的流量确认不同的资源消耗,这种情况我们就需要给服务建立一个资源的评估模型,也就是资源画像,针对服务确认CPU和流量的关系。 这里我们选择最简单的算法,就是线性回归算法。一元线性回归模型可以表示为:$y=β0+β1x$。
- y 是因变量,我们想要预测或解释的变量。
- x 是自变量,我们用来预测因变量的变量。
- β0 是截距项,它是当 𝑥=0,y 的期望值。
- β1 是斜率,表示 x 每变化一个单位,y 预期将如何变化。
线性回归模型的参数,通常通过最小化实际观测值和模型预测值之间的差异来估计。最常用的方法是最小二乘法(Ordinary Least Squares, OLS),它寻找最佳拟合直线,也就是平方误差之和最小的直线。
下面是一个简单的算法实现,首先生成了包含100个样本的假设数据集,其中流量和CPU利用率之间存在线性关系,并添加了正态分布的噪声。然后,它将数据集分为训练集和测试集,创建了一个线性回归模型,并进行了训练和预测。最后,它评估了模型的性能,并可视化了测试数据上的预测结果。接下来我简单介绍一下这个训练步骤。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
# 设置随机种子以获得可重复的结果
np.random.seed(0)
# 生成示例数据
# 假设流量数据和CPU利用率之间存在线性关系,并添加一些随机噪声
traffic = np.random.randint(100, 1000, size=100)
cpu_utilization = 0.05 * traffic + np.random.normal(scale=5, size=100)
# 创建DataFrame
df = pd.DataFrame({
'Traffic': traffic,
'CPU_Utilization': cpu_utilization
})
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
df[['Traffic']],
df['CPU_Utilization'],
test_size=0.2,
random_state=0
)
# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(X_train, y_train)
# 进行预测
y_pred = model.predict(X_test)
# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
# 打印性能指标
print(f'Mean Squared Error: {mse}')
print(f'R-squared: {r2}')
# 可视化结果
plt.scatter(X_test, y_test, color='blue', label='Actual CPU Utilization')
plt.plot(X_test, y_pred, color='red', label='Predicted CPU Utilization', linewidth=2)
plt.xlabel('Traffic')
plt.ylabel('CPU Utilization')
plt.title('Linear Regression Analysis of Traffic and CPU Utilization')
plt.legend()
plt.show()
步骤1:收集相关的数据,通常包括流量数据,通常是QPS,当然也可以是其他的,比如TPS等等。另一个数据CPU利用率,在相同时间间隔内的CPU使用率。确保数据是同步收集的,即流量和CPU利用率数据应该对应相同的时间点或时间段。
步骤2:数据预处理,清洗数据。检查数据集中是否有缺失值或异常值,并进行适当的处理。接下来就是确定哪些特征与CPU利用率相关,这里我们就直接选择了QPS。最后对流量和CPU利用率进行标准化或归一化处理,以消除不同量纲的影响。
步骤3:选择回归模型,如果数据呈现出线性关系,可以选择线性回归模型。如果数据中存在多重共线性或需要进行正则化,可以考虑岭回归。
步骤4:训练模型:使用训练数据集来训练所选的回归模型。在Python中,可以使用具体的库中的回归模型。
步骤5:模型评估。使用均方误差(MSE)、均方根误差(RMSE)和R²分数等指标来评估模型的准确性。使用交叉验证来评估模型的泛化能力。
步骤6:可视化结果,在流量和CPU利用率的散点图上绘制,直观地展示它们之间的关系。
最后,我们把训练出来的参数进行存储,利用存储的参数来预测各个服务在将要面临的资源需求。
从工程领域来看,很多时候我们在预测CPU和QPS的关系时,更多的是关心在高QPS的表现,所以你在进行线性拟合的时候,并不是数据越多越好,可以去选择TOP-N的QPS来进行训练,可能会达到更好的效果。
资源分配
当资源有限的情况下,如何进行合理的资源分配可以让吞吐最大化,这里我们回顾一下前面的一个场景。并不是所有服务都进行扩容,而是某几条链路扩容,这里就需要分析这条链路上有哪些服务,以及相关服务的扩容比例。这里我来说一下其中的一种比较复杂的情况,链路之间存在交叉调用。比如链路A1服务同时调用了A2和B2,你可以看一下示意图。
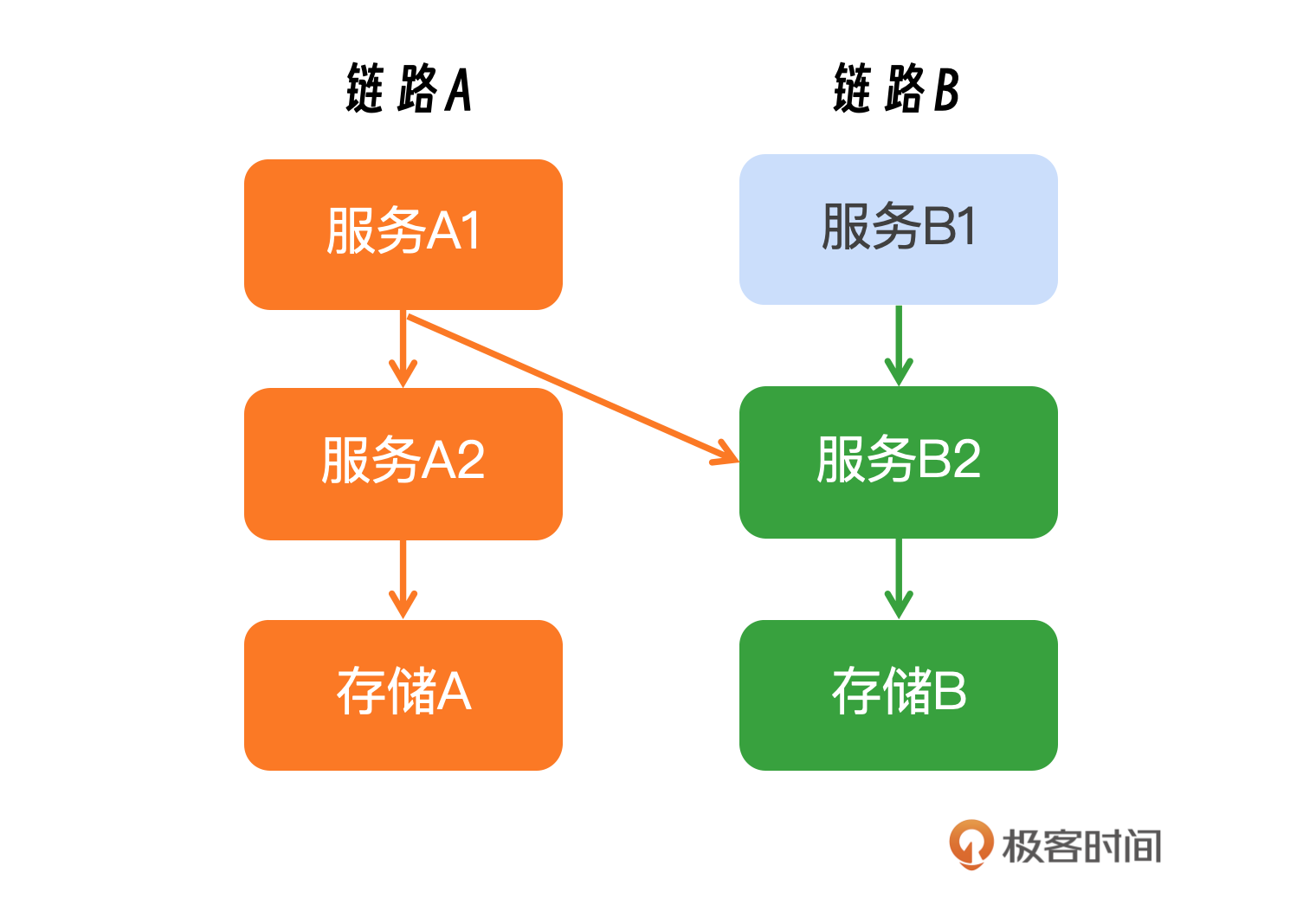
在进行服务链路管理和扩容规划时,首先要全面识别出链路上所有涉及的服务,这包括直接依赖和间接依赖的服务。为了更直观地展示这一过程,我提供了一张表格作为参考,帮助你进一步理解。
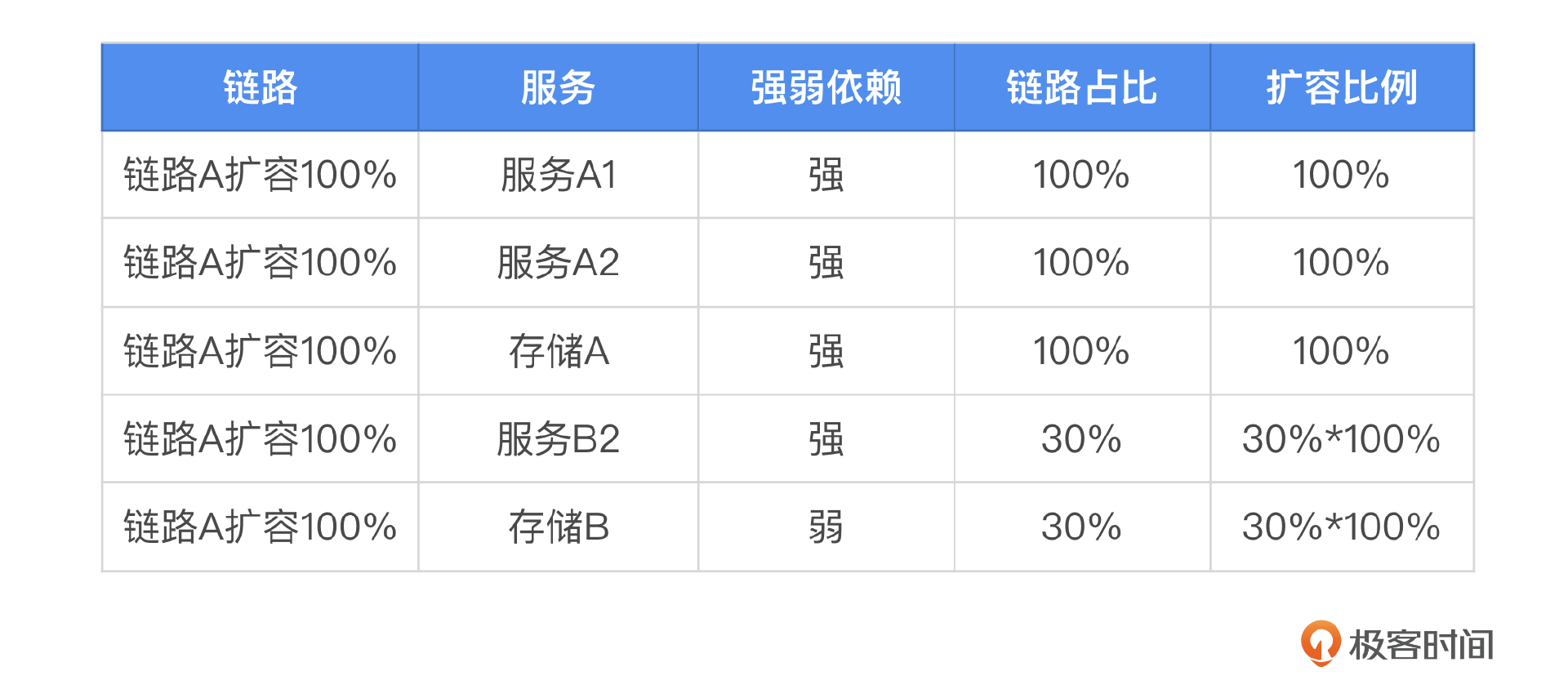
这个时候我们最常见的做法其实就是应用贪心算法,根据服务的重要等级、强弱依赖使用贪心算法进行资源分配。
步骤 1:定义服务的属性
- 重要等级:为每个服务分配一个重要等级,数值越大表示服务越重要。
- 资源需求:确定每个服务所需的资源量。
- 依赖关系:明确服务之间的依赖关系,某些服务可能只有在其他服务运行后才能正常工作。
步骤 2:服务排序
根据服务的重要等级对所有服务进行排序。如果有依赖关系,还需要考虑这些依赖关系,确保高优先级的服务或关键依赖服务能够优先分配资源。
步骤 3:资源分配
设置当前可用资源为总资源,然后从排序后的列表中选择当前最重要且尚未分配资源的服务。如果服务的资源需求小于或等于当前可用资源,则为服务分配所需资源,并更新当前可用资源。如果服务的资源需求大于当前可用资源,就跳过这个服务,考虑下一个重要等级的服务。
步骤4:继续分配
重复步骤3,直到所有服务都被考虑过或资源耗尽。如果存在剩余资源,可以考虑重新分配给那些资源需求未被完全满足的服务。
贪心算法实现简单、执行效率高,适用于多种场景,特别是在问题规模较小的情况下。不过,面对更复杂的问题,我们可能需要探索动态规划、线性规划或其他高级优化算法。
class ResourceAllocator:
def __init__(self, total_resources):
self.total_resources = total_resources
self.allocated_resources = 0
def can_allocate(self, resource_need):
return resource_need <= self.total_resources - self.allocated_resources
def allocate_resources(self, service):
if self.can_allocate(service['resource_need']):
self.allocated_resources += service['resource_need']
print(f"Allocated {service['resource_need']} resources to {service['name']}")
return True
else:
print(f"Not enough resources to allocate to {service['name']}")
return False
def allocate_all(self, services):
# 按重要等级排序服务
services.sort(key=lambda x: x['importance'], reverse=True)
# 分配资源给所有服务
for service in services:
self.allocate_resources(service)
# 假设有以下服务,每个服务有其重要等级和资源需求
services = [
{'name': 'Service A', 'importance': 3, 'resource_need': 10},
{'name': 'Service B', 'importance': 2, 'resource_need': 5},
{'name': 'Service C', 'importance': 4, 'resource_need': 8},
# 添加更多服务...
]
# 创建资源分配器实例,假设总资源为20
allocator = ResourceAllocator(total_resources=20)
# 分配资源给所有服务
allocator.allocate_all(services)
# 打印剩余资源
print(f"Remaining resources: {allocator.total_resources - allocator.allocated_resources}")
__init__:初始化函数,设置总资源和已分配资源。can_allocate:检查是否可以为特定服务分配资源。allocate_resources:尝试为单个服务分配资源。allocate_all:按重要等级排序服务,并尝试为所有服务分配资源。
小结
这节课我重点介绍了三个关键场景,和它们对应的基础算法,这些基础算法在日常办公和工程实践中已被证明是非常高效的。当然也存在更复杂的算法,比如线性规划,动态规划等等。对这些算法的探索和应用将留给你们在未来的学习中进一步深入。

思考题
当你在进行资源画像的时候,你发现机器的型号不一样,资源和流量的对应关系也不一样,遇到这种情况你会如何处理呢?欢迎你把你的答案分享到评论区,也欢迎你把这节课的内容分享给其他朋友,我们下节课再见!