44 奇异值分解：如何挖掘潜在的语义关系？

你好，我是黄申。

今天，我们来聊另一种降维的方法，SVD奇异值分解（Singular Value Decomposition）。它的核心思路和PCA不同。PCA是通过分析不同维度特征之间的协方差，找到包含最多信息量的特征向量，从而实现降维。而SVD这种方法试图通过样本矩阵本身的分解，找到一些“潜在的因素”，然后通过把原始的特征维度映射到较少的潜在因素之上，达到降维的目的。

这个方法的思想和步骤有些复杂，它的核心是矩阵分解，首先，让我们从方阵的矩阵分解开始。

方阵的特征分解

在解释方阵的分解时，我们会用到两个你可能不太熟悉的概念：方阵和酉矩阵。为了让你更顺畅的理解整个分解的过程，我先给你解释下这两个概念。

方阵（Square Matrix）是一种特殊的矩阵，它的行数和列数相等。如果一个矩阵的行数和列数都是n，那么我们把它称作n阶方阵。

如果一个矩阵和其转置矩阵相乘得到的是单位矩阵，那么它就是一个酉矩阵（Unitary Matrix）。

$X’X=I$

其中X’表示X的转置，I表示单位矩阵。换句话说，矩阵X为酉矩阵的充分必要条件是X的转置矩阵和X的逆矩阵相等。

$X’=X^{-1}$

理解这两个概念之后，让我们来观察矩阵的特征值和特征向量。前两节我们介绍了，对于一个n×n维的矩阵$X$，$n$维向量$v$，标量$λ$，如果有$Xv=λv$。

那么我们就说$λ$是$X$的特征值，$v$是$X$的特征向量，并对应于特征值$λ$。

之前我们说过特征向量表示了矩阵变化的方向，而特征值表示了变化的幅度。实际上，通过特征值和特征矩阵，我们还可以把矩阵X进行特征分解（Eigendecomposition）。这里矩阵的特征分解，是指把矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。如果我们求出了矩阵$X$的$k$个特征值$λ1，λ2，…，λn$，以及这$n$个特征值所对应的特征向量$v1，v2，…，vn$，那么就有$XV=VΣ$。

其中，$V$是这$n$个特征向量所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵。进一步推导，我们可以得到：

$XVV^{-1}=VΣV$
$XI=VΣV^{{-1}$

$X=VΣV}$

如果我们会把$V$的这$n$个特征向量进行标准化处理，那么对于每个特征向量$V_i$，就有$||V_i||_2=1$，而这表示$V’_iV_i=1$，此时V的n个特征向量为标准正交基，满足$V’V=I$ ，也就是说V为酉矩阵，有$V’=V^{-1}$ 。这样一来，我们就可以把特征分解表达式写作$X=VΣV’$。

我们以介绍PCA分析时所用的矩阵为例，验证矩阵的特征分解。当时，我们有一个：

下面我们需要证明$X=VΣV’$成立，我把推算的过程写在下面了。

讲到这里，相信你对矩阵的特征分解有了一定程度的认识。可是，矩阵$X$必须为对称方阵才能进行有实数解的特征分解。那么如果$X$不是方阵，那么应该如何进行矩阵的分解呢？这个时候就需要用到奇异值分解SVD了。

矩阵的奇异值分解

SVD分解和特征分解相比，在形式上是类似的。假设矩阵$X$是一个m×n维的矩阵，那么$X$的SVD为$X=UΣV’$。

不同的地方在于，SVD并不要求要分解的矩阵为方阵，所以这里的$U$和$V’$并不是互为逆矩阵。其中$U$是一个m×m维的矩阵，$V$是一个n×n维的矩阵。而$Σ$是一个m×n维的矩阵，对于$Σ$来说，只有主对角线之上的元素可以为非$0$，其他元素都是$0$，而主对角线上的每个元素就称为奇异值。$U$和$V$都是酉矩阵，即满足$U’U=I,V’V=I$。

现在问题来了，我们应该如何求出，用于SVD分解的$U,Σ和V$这三个矩阵呢？之所以不能使用有实数解的特征分解，是因为此时矩阵X不是对称的方阵。我们可以把$X$的转置$X’$和$X$做矩阵乘法，得到一个n×n维的对称方阵$X’X$。这个时候，我们就能对$X’X$这个对称方阵进行特征分解了，得到的特征值和特征向量满足$(XX’)v_i=λ_iv_i$。

这样一来，我们就得到了矩阵$X’X$的$n$个特征值和对应的$n$个特征向量$v$。通过$X’X$的所有特征向量构造一个n×n维的矩阵$V$，这就是上述SVD公式里面的$V$矩阵了。通常我们把$V$中的每个特征向量叫作$X$的右奇异向量。

同样的道理，如果我们把X和X’做矩阵乘法，那么会得到一个m×m维的方阵XX’。由于XX’也是方阵，因此我们同样可以对它进行特征分解，得到的特征值和特征向量满足$(XX’)u_i=λ_iu_i$。

类似地，我们得到了矩阵$XX’$的m个特征值和对应的m个特征向量$u$。通过XX’的所有特征向量构造一个m×m的矩阵$U$。这就是上述SVD公式里面的$U$矩阵了。通常，我们把U中的每个特征向量叫作X的左奇异向量。

现在，包含左右奇异向量的$U$和$V$都求解出来了，只剩下奇异值矩阵$Σ$了。之前我提到，$Σ$除了对角线上是奇异值之外，其他位置的元素都是$0$，所以我们只需要求出每个奇异值$σ$就可以了。这个解可以通过下面的公式推导求得：

$X=UΣV’$
$XV=UΣV’V$

由于$V$是酉矩阵，所以$V’V=I$，就有：

$XV=UΣI$
$XV=UΣ$
$Xv_i=σ_iu_i$
$σ_i=\frac{Xv_i}{u_i}$

其中$v_i$和$u_i$都是列向量。一旦我们求出了每个奇异值$σ$，那么就能得到奇异值矩阵$Σ$。

通过上述几个步骤，我们就能把一个mxn维的实数矩阵，分解成$X=UΣV’$的形式。说到这里，你可能会疑惑，把矩阵分解成这个形式有什么用呢？实际上，在不同的应用中，这种分解表示了不同的含义。下面，我会使用潜在语义分析的案例，带你看看，在发掘语义关系的时候，SVD分解起到了怎样的关键作用。

潜在语义分析和SVD

在讲向量空间模型的时候，我解释了文档和词条所组成的矩阵。对于一个大的文档集合，我们首先要构造字典，然后根据字典构造每篇文档的向量，最后通过所有文档的向量构造矩阵。矩阵的行和列分别表示文档和词条。基于这个矩阵、向量空间中的距离、余弦夹角等度量，我们就可以进行基于相似度的信息检索或文档聚类。

不过，最简单的向量空间模型采用的是精确的词条匹配，它没有办法处理词条形态的变化、同义词、近义词等情况。我们需要使用拉丁语系的取词根（Stemming）操作，并手动建立同义词、近义词词典。这些处理方式都需要人类的语义知识，也非常依赖人工的干预。另外，有些词语并不是同义词或者近义词，但是相互之间也是有语义关系的。例如“学生”“老师”“学校”“课程”等等。

那么，我们有没有什么模型，可以自动地挖掘在语义层面的信息呢？当然，目前的计算机还没有办法真正理解人类的自然语言，它们需要通过大量的数据，来找到词语之间的关系。下面我们就来看看潜在语义分析LSA（Latent Semantic Analysis）或者叫潜在语义索引LSI（Latent Semantic Index）这种方法，是如何做到这点的。

和一般的向量空间模型有所不同，LSA通过词条和文档所组成的矩阵，发掘词和词之间的语义关系，并过滤掉原始向量空间中存在的一些“噪音”，最终提高信息检索和机器学习算法的精确度。LSA主要包括以下这些步骤。

第一步，分析文档集合，建立表示文档和词条关系的矩阵。

第二步，对文档-词条矩阵进行SVD奇异值分解。在LSA的应用场景下，分解之后所得到的奇异值σ对应了一个语义上的“概念”，而$σ$值的大小表示这个概念在整个文档集合中的重要程度。$U$中的左奇异值向量表示了每个文档和这些语义“概念”的关系强弱，$V$中的右奇异值向量表示每个词条和这些语义“概念”的关系强弱。所以说，SVD分解把原来的词条-文档关系，转换成了词条-语义概念-文档关系。

我画了一张图帮助你理解这个过程。

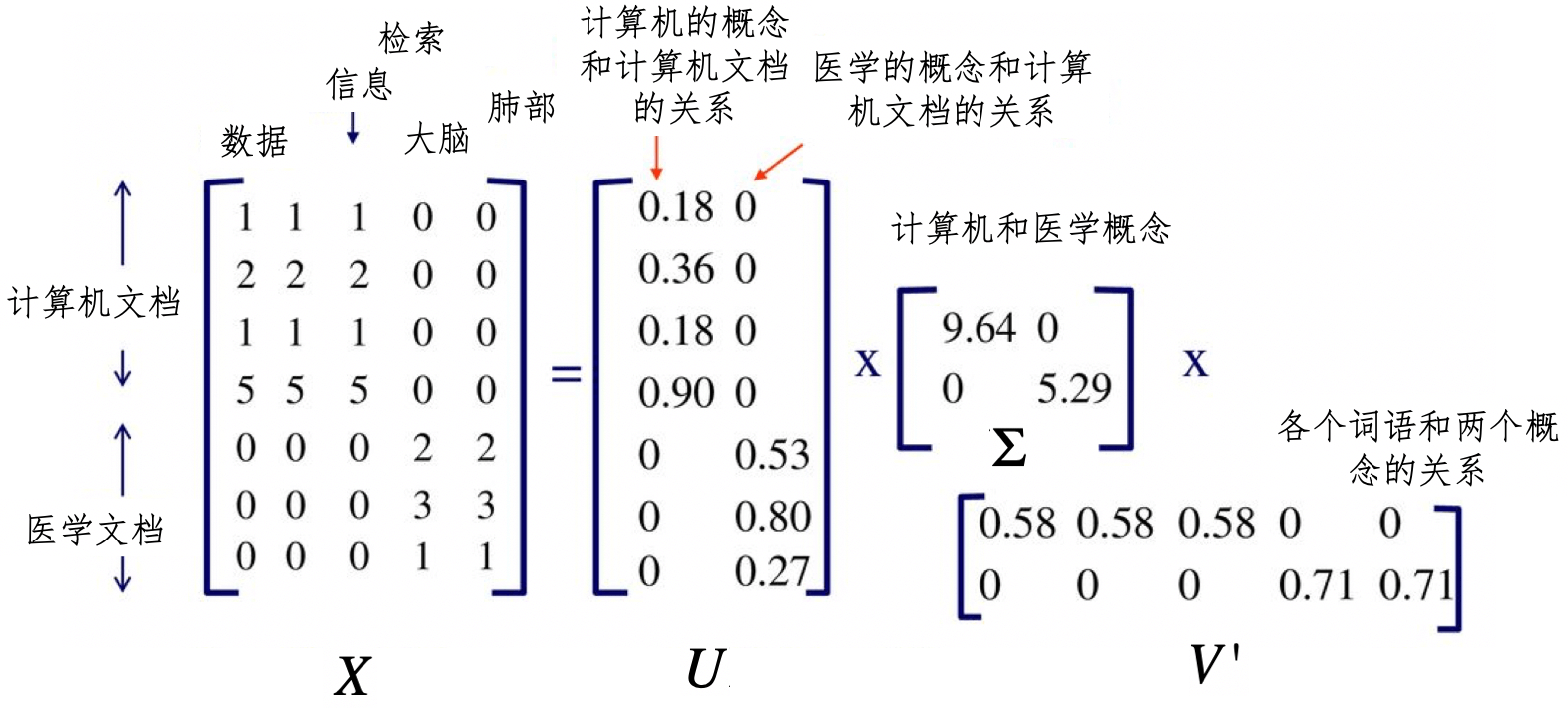
在这张图中，我们有一个7×5维的矩阵$X$，表示7个文档和5个单词。经过SVD分解之后，我们得到了两个主要的语义概念，一个概念描述了计算机领域，另一个概念描述了医学领域。矩阵U描述文档和这两个概念之间的关系，而矩阵$V’$描述了各个词语和这两个概念之间的关系。如果要对文档进行检索，我们可以使用$U$这个降维之后的矩阵，找到哪些文档和计算机领域相关。同样，对于聚类算法，我们也可以使用U来判断哪些文档属于同一个类。

第三步，对SVD分解后的矩阵进行降维，这个操作和PCA主成分分析的降维操作是类似的。

第四步，使用降维后的矩阵重新构建概念-文档矩阵，新矩阵中的元素不再表示词条是不是出现在文档中，而是表示某个概念是不是出现在文档中。

总的来说，LSA的分解，不仅可以帮助我们找到词条之间的语义关系，还可以降低向量空间的维度。在这个基础之上再运行其他的信息检索或者机器学习算法，就更加有效。

总结

之前介绍的PCA主成分分析，要求矩阵必须是对称的方阵，因此只适用于刻画特征之间关系的协方差矩阵。但是，有的时候我们需要挖掘的是样本和特征之间的关系，例如文档和词条。这个时候矩阵并不是对称的方阵，因此无法直接使用PCA分析。

为此，SVD奇异值分解提供了一种可行的方案。它巧妙地运用了矩阵X和自己的转置相乘，生成了两种对称的方阵，并通过这两者的特征分解，获得了SVD中的左奇异向量所组成的矩阵U和右奇异向量所组成的矩阵V，并最终推导出奇异值矩阵Σ。这样，SVD就可以对原始的数据矩阵进行分解，并运用最终的奇异向量进行降维。

我们可以把SVD运用在很多场合中，在不同的应用场景下，$U，V$和$Σ$代表了不同的含义。例如，在LSA分析中，通过对词条和文档矩阵的SVD分解，我们可以利用Σ获得代表潜在语义的一些概念。而矩阵$U$表示了这些概念和文档之间的关系，矩阵$V$表示了这些概念和单个词语之间的关系。

思考题

请使用你自己熟悉的语言实现SVD分解。（提示：如果使用Python等科学计算语言，你可以参考本节所讲述的矩阵分解步骤，也可以使用一些现成的科学计算库。）

欢迎留言和我分享，也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”，把今天的内容分享给你的好友，和他一起精进。

精选留言（15）

南边 👍（2） 💬（3）
把 V 的这 n 个特征向量进行标准化处理，那么对于每个特征向量 Vi，就有 ∣∣Vi∣∣2=1，而这表示 V’iVi=1，此时 V 的 n 个特征向量为标准正交基，满足 V’V=I ，也就是说 V 为酉矩阵对于V是酉矩阵这个推导还是不太理解
2020-01-16

qinggeouye 👍（2） 💬（2）
import numpy as np from numpy import linalg as la # 文档集合文档和词条关系矩阵行表示文档列表示词条 x = np.mat([[1, 1, 1, 0, 0], [2, 2, 2, 0, 0], [1, 1, 1, 0, 0], [5, 5, 5, 0, 5], [0, 0, 0, 2, 2], [0, 0, 0, 3, 3], [0, 0, 0, 1, 1]]) U, sigma, VT = la.svd(x) print(U, "\n") print(sigma, "\n") print(VT, "\n") S = np.zeros((7, 5)) # 奇异矩阵 for i in range(len(sigma)): S[i, i] = sigma[i] print(" 与矩阵 x 一致？ \n", U.dot(S).dot(VT.transpose())) 这里计算出的左奇异矩阵、奇异值矩阵、右奇异值矩阵，以及它们的点乘，与本文中的都不太一样，不知哪里出问题了？
2019-04-03

！null 👍（1） 💬（1）
U 是一个 m×m 维的矩阵，V 是一个 n×n 维的矩阵。而 Σ 是一个 m×n 维的矩阵上边m×m和n×n意思是m阶和n阶方阵吗？如果是，为什么lsa的例子里，就是计算机文档和医学文档的例子里，U和V都不是方阵，而 Σ 是个方阵？
2021-08-30

！null 👍（1） 💬（1）
σ[i]=(X*v[i])/u[i] 这个公式后边怎么算没看懂。X应该是最开始的矩阵，v[i]和u[i]是特征向量吗？那X*u[i]结果应该也是向量。最后就是两个向量之间做除法。向量间除法应该怎么算？
2021-08-30

！null 👍（1） 💬（1）
其中 U 是一个 m×m 维的矩阵，V 是一个 n×n 维的矩阵。而 Σ 是一个 m×n 维的矩阵，对于 Σ 来说，只有主对角线之上的元素可以为非 0，其他元素都是 0，而主对角线上的每个元素就称为奇异值。后边“计算机文档和医学文档”奇异值分解之后，没觉得U是 m×m 维的矩阵，V 是一个 n×n 维的矩阵，Σ 是一个 m×n 维的矩阵。如果Σ有对角线的话，是不是Σ 应该是个方阵？
2021-08-23

Paul Shan 👍（1） 💬（2）
文档例子和svd分解有差别，svd是左右为方阵，中间为非方阵。文档例子是中间为方阵，左右为方阵，我感觉这里缺了一步，是不是文档的例子已经是降维后的结果了？
2019-10-11

marcus1877 👍（0） 💬（1）
“第三步，对 SVD 分解后的矩阵进行降维，这个操作和 PCA 主成分分析的降维操作是类似的。” 是对SVD分解后的U,V',∑ 降维吗？
2021-03-31

建强 👍（0） 💬（1）
思考题：请教一下老师，SVD中的奇异值矩阵，能否用U'XV来计算，因为UU'=I, 所以对于等式X = UΣV'，分别用U'和V对等式两边进行左乘和右乘，就得到Σ = U'XV，不知这样推导是否正确？用Python简单写了一个SVD分解的程序，源代码如下： def SVD_Solve(X): # 计算U矩阵 = XX'的特征矩阵 U = X.dot(X.T) U_feature, U_vector = LA.eig(U) # 计算V矩阵 = X'X的特征矩阵 V = X.T.dot(X) V_feature, V_vector = LA.eig(V) # 计算西格码对角矩阵 = U'XV XGM = (U_vector.T.dot(X)).dot(V_vector) return U_vector, XGM, V_vector.T #测试 X = mat([[1,1,1,0,0] ,[2,2,2,0,0] ,[1,1,1,0,0] ,[5,5,5,0,0] ,[0,0,0,2,2] ,[0,0,0,3,3] ,[0,0,0,1,1] ] ) U,XGM,V = SVD_Solve(X) print("左奇异向量\n","="*10, "\n", U) print("奇异值矩阵\n","="*10, "\n", XGM) print("右奇异向量\n","="*10, "\n", V)
2020-11-29

不接地气的马三岁 👍（0） 💬（3）
算方差的时候，不应该还有个1/N吗，N是元素个数，(x1-0)^2+...+(xn-0)^2为什么不等于N。
2020-07-21

骑行的掌柜J 👍（0） 💬（1）
又get到一个新的知识点奇异值SVD😁虽然有疑惑这里“就有 ∣∣Vi∣∣2=1，而这表示 V’iVi=1，此时 V 的 n 个特征向量为标准正交基” 不过已经有好几个朋友提问出来老师也解答了剩下就是熟练这个过程谢谢黄老师 PS: 如果有SVD奇异值分解项目案例就更好了
2020-07-09

罗耀龙@坐忘 👍（0） 💬（1）
茶艺师学编程到这里，总算看到了在大学时算的死去活来的求逆矩阵、矩阵相乘、矩阵变换的一个应用……
2020-05-18

灰太狼 👍（0） 💬（1）
如果我们会把 V 的这 n 个特征向量进行标准化处理，那么对于每个特征向量 V_i，就有 ||V_i||_2=1，而这表示 V’_iV_i=1，此时 V 的 n 个特征向量为标准正交基，满足 V’V=I ，也就是说 V 为酉矩阵，有 V’=V^{-1} 。这样一来，我们就可以把特征分解表达式写作 X=VΣV’。 -------------------------- 黄老师，接着上一个问题，我还是有点疑问，这个地方特征向量进行了标准化，这个标准化是在原始矩阵上对每个列向量进行的标准化吗？还是在哪儿做的标准化？如果原始矩阵没做标准化，求出特征向量后又进行标准化那应该不再是原始矩阵的特征向量了吧？
2020-04-06

灰太狼 👍（0） 💬（1）
如果我们会把 V 的这 n 个特征向量进行标准化处理，那么对于每个特征向量 V_i，就有 ||V_i||_2=1，而这表示 V’_iV_i=1，此时 V 的 n 个特征向量为标准正交基，满足 V’V=I ， -------------- 黄老师，这个地方有点没太看懂，请问这儿的标准化是在什么时候做的？如果不做标准化等式是不是就不成立了？
2020-04-03

wick 👍（0） 💬（1）
老师好，文中奇异值 σ的求解，由XV=UΣ推出Xvi=σiui再到σi=uiXvi没懂
2020-03-13

013923 👍（1） 💬（0）
学习了新知识，谢谢！
2022-09-15