11 树的深度优先搜索（上）：如何才能高效率地查字典？

你好，我是黄申。

你还记得迭代法中的二分查找吗？在那一讲中，我们讨论了一个查字典的例子。如果要使用二分查找，我们首先要把整个字典排个序，然后每次都通过二分的方法来缩小搜索范围。

不过在平时的生活中，咱们查字典并不是这么做的。我们都是从单词的最左边的字母开始，逐个去查找。比如查找“boy”这个单词，我们一般是这么查的。首先，在a～z这26个英文字母里找到单词的第一个字母b，然后在b开头的单词里找到字母o，最终在bo开头的单词里找到字母y。

你可以看我画的这种树状图，其实就是从树顶层的根结点一直遍历到最下层的叶子结点，最终逐步构成单词前缀的过程。对应的数据结构就是前缀树（prefix tree），或者叫字典树（trie）。我个人更喜欢前缀树这个名称，因为看到这个名词，这个数据结构的特征就一目了然。

那前缀树究竟该如何构建呢？有了前缀树，我们又该如何查询呢？今天，我会从图论的基本概念出发，来给你讲一下什么样的结构是树，以及如何通过树的深度优先搜索，来实现前缀树的构建和查询。

图论的一些基本概念

前缀树是一种有向树。那什么是有向树？顾名思义，有向树就是一种树，特殊的就是，它的边是有方向的。而树是没有简单回路的连通图。

如果一个图里所有的边都是有向边，那么这个图就是有向图。如果一个图里所有的边都是无向边，那么这个图就是无向图。既含有向边，又含无向边的图，称为混合图。

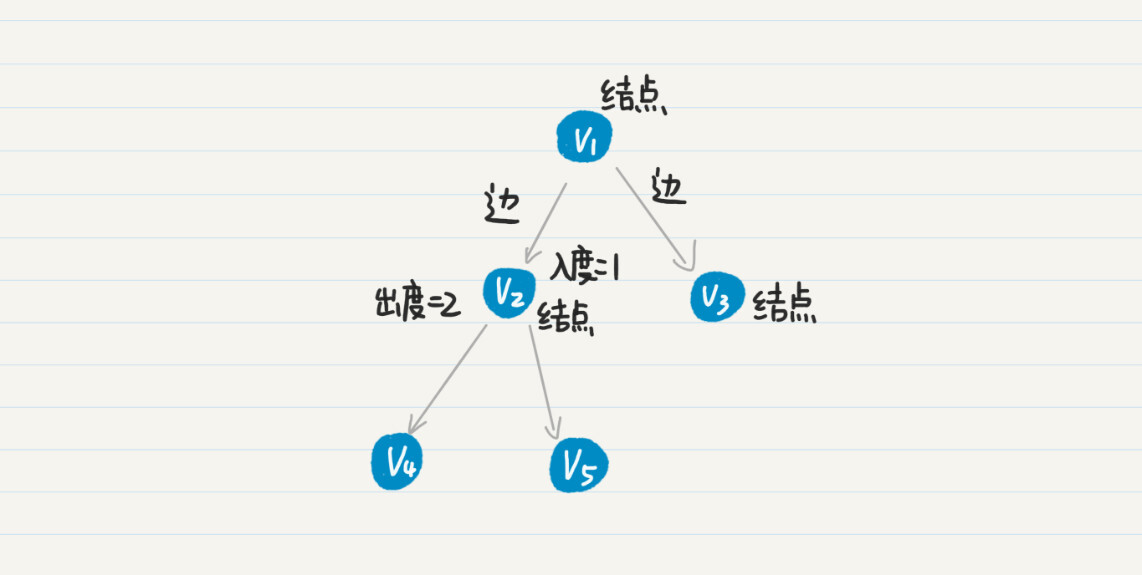
在有向图中，以结点$v$为出发点的边的数量，我们叫作$v$的出度。而以$v为$终点的边之数量，称为$v$的入度。在上图中，结点$v_{2}$的入度是1，出度是2。

还有两个和有向树有关的概念，回路和连通，我这里简单给你解释一下，你很容易就能明白了。

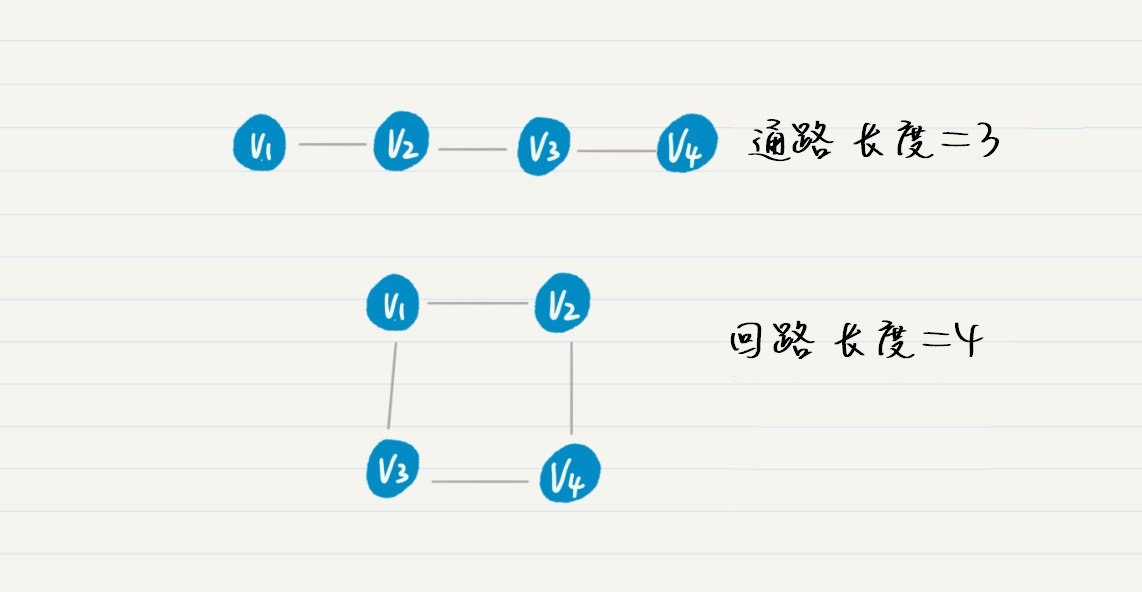
结点和边的交替序列组成的就是通路。所以，通路上的任意两个结点其实就是互为连通的。如果一条通路的起始点$v_{1}$和终止点$v_{n}$相同，这种特殊的通路我们就叫作回路。从起始点到终止点所经过的边之数量，就是通路的长度。这里我画了一张图，这里面有1条通路和1条回路，第一条非回路通路的长度是3，第二条回路的长度是4。

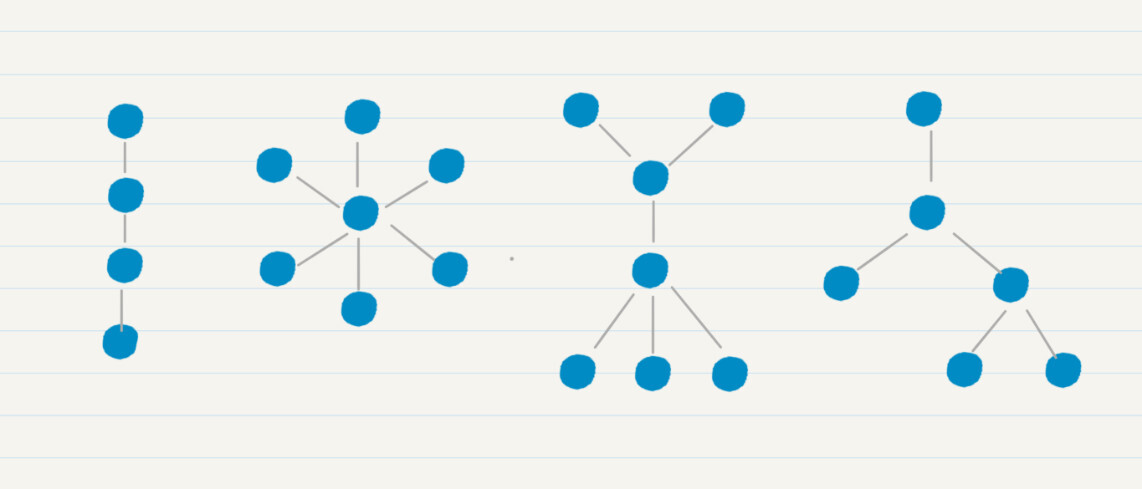
理解了图的基本概念，我们再来看树和有向树。树是一种特殊的图，它是没有简单回路的连通无向图。这里的简单回路，其实就是指，除了第一个结点和最后一个结点相同外，其余结点不重复出现的回路。你可以看我画的这几幅图。

那么，什么是有向树呢？顾名思义，有向树是一种特殊的树，其中的边都是有向的，而且它满足以下几个条件：

• 有且仅有一个结点的入度为0，这个结点被称为根；
• 除根以外的所有结点，入度都为1。从树根到任一结点有且仅有一条有向通路。

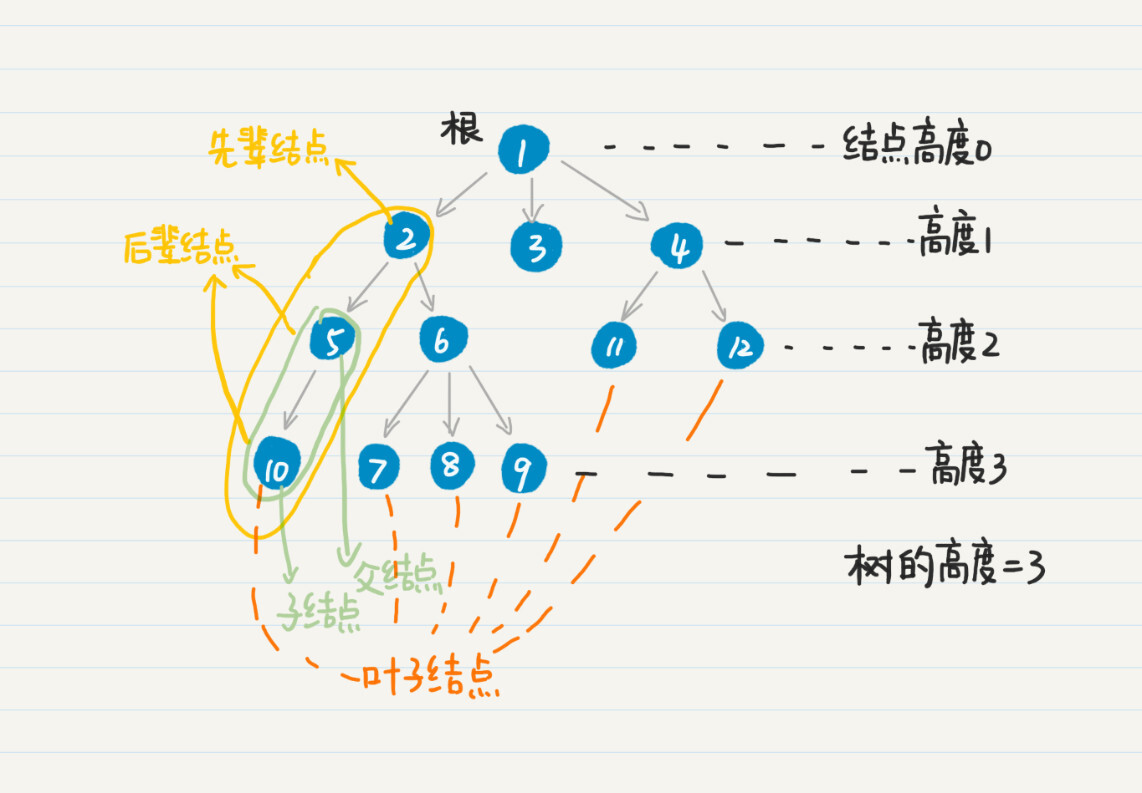
除了这些基本定义，有向树还有几个重要的概念，父结点、子结点、兄弟结点、先辈结点、后辈结点、叶子结点、结点的高度（或深度）、树的高度（或深度）。这些都不难理解，我画个图展示一下，你就能明白了。我把根结点的高度设置为0，根据需要你也可以设置为1。

前缀树的构建和查询

好了，说了这么些，你对有向树应该有了理解。接下来，我们来看，如何使用有向树来实现前缀树呢？这整个过程主要包括两个部分：构建前缀树和查询前缀树。

1. 构建前缀树

首先，我们把空字符串作为树的根。对于每个单词，其中每一个字符都代表了有向树的一个结点。而前一个字符就是后一个字符的父结点，后一个字符是前一个字符的子结点。这也意味着，每增加一个字符，其实就是在当前字符结点下面增加一个子结点，相应地，树的高度也增加了1。

我们以单词geek为例，从根结点开始，第一次我增加字符g，在根结点下增加一个“g”的结点。第二次，我在“g”结点下方增加一个“e”结点。以此类推，最终我们可以得到下面的树。

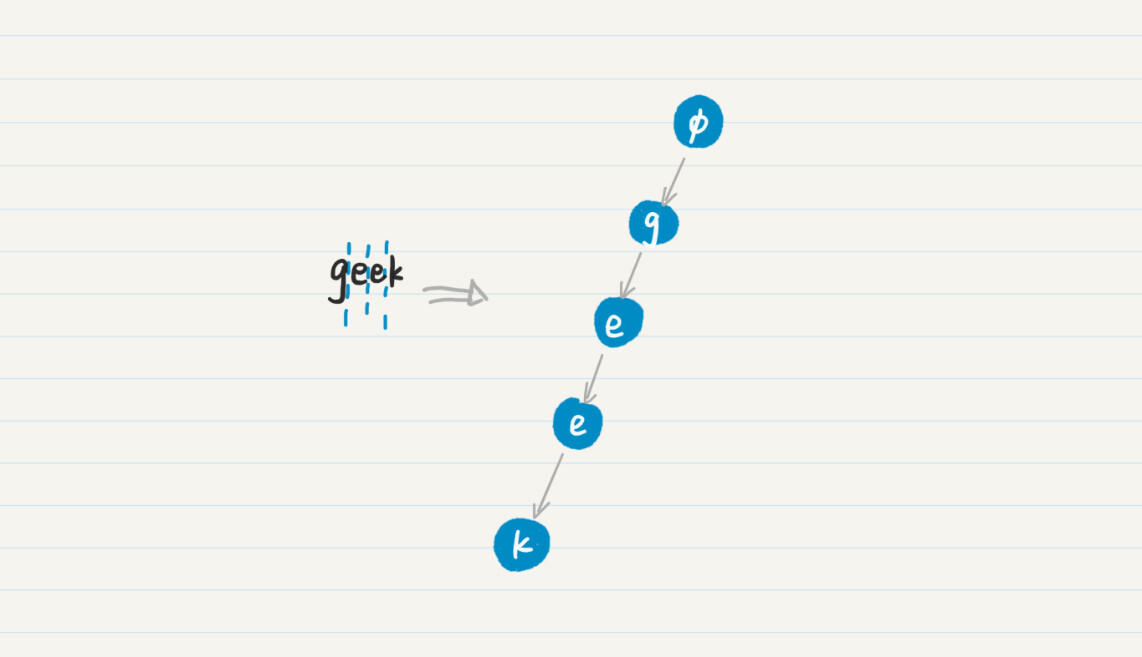
那如果这个时候，再增加一个单词，geometry会怎样？我们继续重复这个过程，就能得到下面这个图。

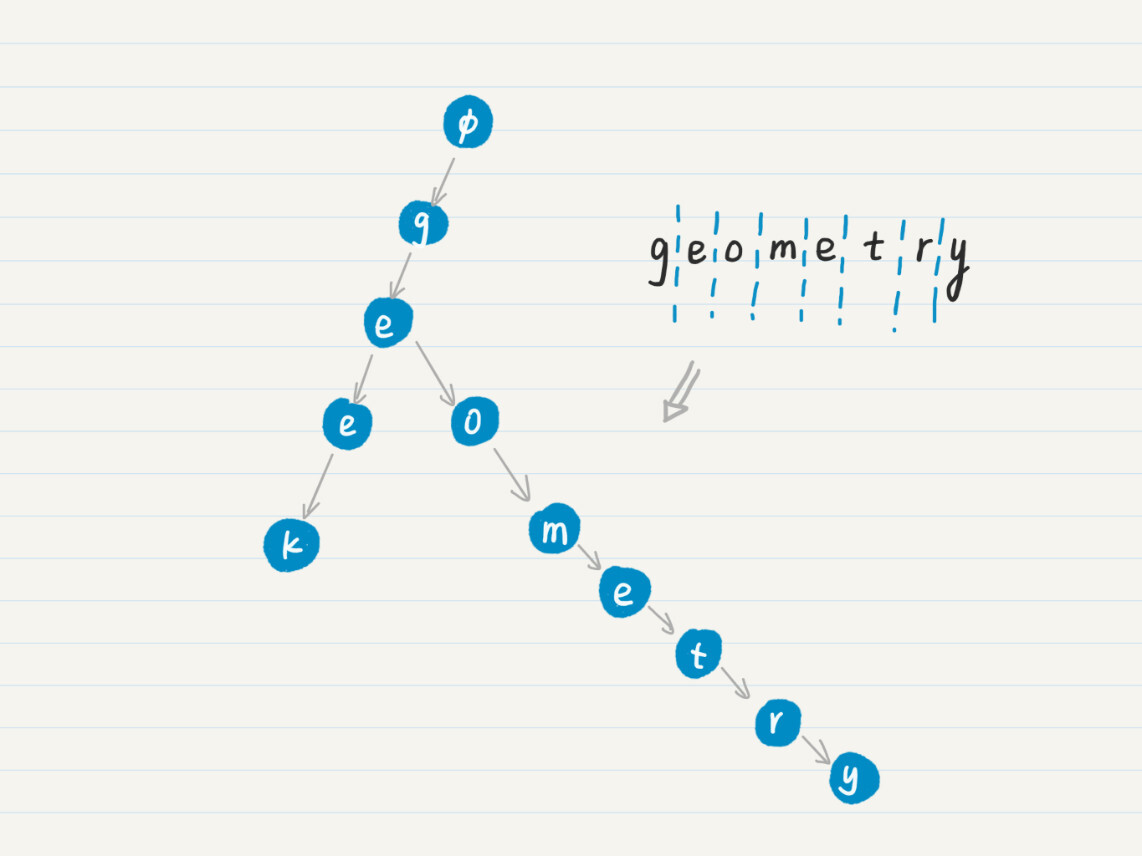
到这里为止，我们已经建立了包含两个单词的前缀树。在这棵树的两个叶子结点“k”和“y”上，我们可以加上额外的信息，比如单词的解释。那么在匹配成功之后，就可以直接返回这些信息，实现字典的功能了。假设我把牛津词典里所有的英文单词都按照上述的方法处理一遍，就能构造一棵包含这个字典里所有单词的前缀树，并实现常用单词的查找和解释。

2. 查询前缀树

假设我们已经使用牛津词典，构建完了一个完整的前缀树，现在我们就能按照开篇所说的那种方式，查找任何一个单词了。从前缀树的根开始，查找下一个结点，顺着这个通路走下去，一直走到某个结点。如果这个结点及其前缀代表了一个存在的单词，而待查找的单词和这个结点及其前缀正好完全匹配，那就说明成功找到了一个单词。否则，就表示无法找到。

这里还有几种特殊情况，需要注意。

• 如果还没到叶子结点的时候，待查的单词就结束了。这个时候要看最后匹配上的非叶子结点是否代表一个单词；如果不是，那说明被查单词并不在字典中。
• 如果搜索到前缀树的叶子结点，但是被查单词仍有未处理的字母。由于叶子结点没有子结点，这时候，被查单词不可能在字典中。
• 如果搜索到一半，还没到达叶子结点，被查单词也有尚未处理的字母，但是当前被处理的字母已经无法和结点上的字符匹配了。这时候，被查单词不可能在字典中。

前缀树的构建和查询这两者在本质上其实是一致的。构建的时候，我们需要根据当前的前缀进行查询，然后才能找到合适的位置插入新的结点。而且，这两者都存在一个不断重复迭代的查找过程，我们把这种方式称为深度优先搜索（Depth First Search）。

所谓树的深度优先搜索，其实就是从树中的某个结点出发，沿着和这个结点相连的边向前走，找到下一个结点，然后以这种方式不断地发现新的结点和边，一直搜索下去，直到访问了所有和出发点连通的点、或者满足某个条件后停止。

如果到了某个点，发现和这个点直接相连的所有点都已经被访问过，那么就回退到在这个点的父结点，继续查看是否有新的点可以访问；如果没有就继续回退，一直到出发点。由于单棵树中所有的结点都是连通的，所以通过深度优先的策略可以遍历树中所有的结点，因此也被称为深度优先遍历。

为了让你更容易理解，我用下面这张图来展示在一棵有向树中进行深度优先搜索时，结点被访问的顺序。

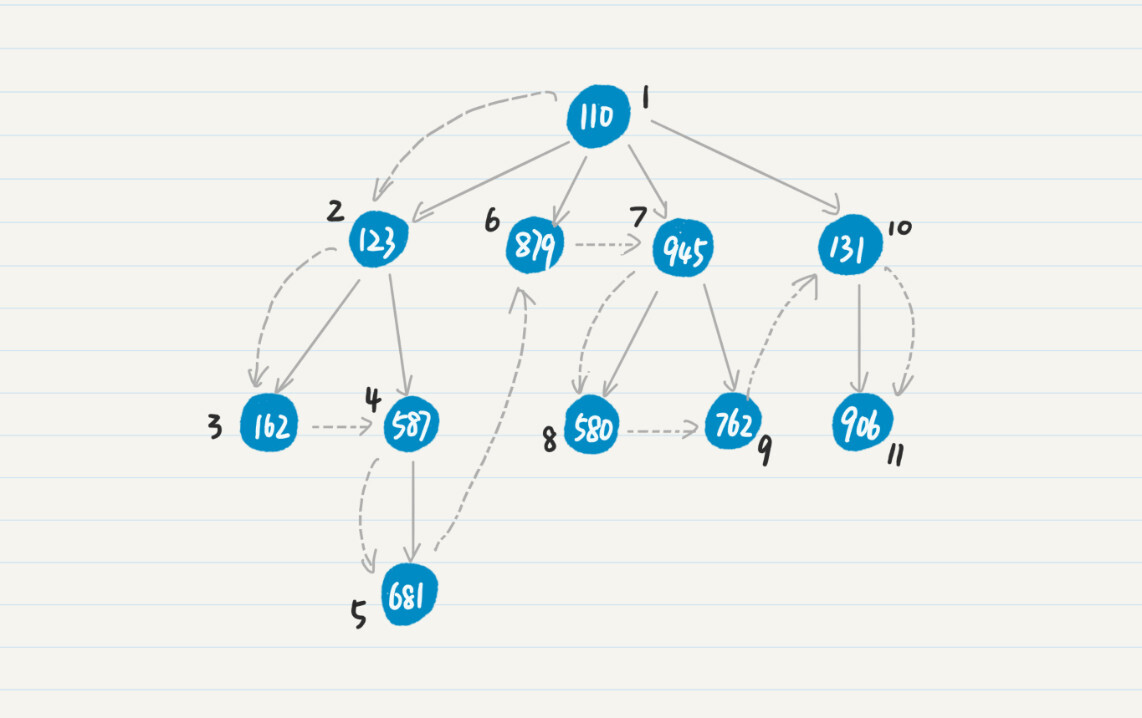
其中，结点上的数字表示结点的ID，而虚线表示遍历前进的方向，结点边上的数字表示该结点在深度优先搜索中被访问的顺序。在深度优先的策略下，我们从点110出发，然后发现和110相连的点123，访问123后继续发现和123相连的点162，再往后发现162没有出度，因此回退到123，查看和123相连的另一个点587，根据587的出度继续往前推进，如此类推。

把深度优先搜索，和在前缀树中查询单词的过程对比一下，你就会发现两者的逻辑是一致的。不过，使用前缀树匹配某个单词的时候，只需要沿着一条可能的通路搜索下去，而无需遍历树中所有的结点。

小结

在这一讲，我从数学中图的一些基本定义入手，介绍了有向树，以及有向树的一个应用，前缀树。树在计算机领域中运用非常广泛。比如，二叉树和满二叉树。

二叉树是每个结点最多有两个子树的树结构，它可用于二叉查找树和二叉堆。二叉树甚至可以用于图示化我们之前聊过的二分迭代。

满二叉树是一棵高度为n（高度从1开始计），且有2^{n-1个结点的二叉树。在高度为k(0<k≤n）的这一层上，结点的数量为2}(k-1)。如果把树的根标为0，每个结点的左子结点标为0，每个结点的右子结点标为1，那么把根到叶子结点的所有0或1连起来，就正好对应一个二进制数。

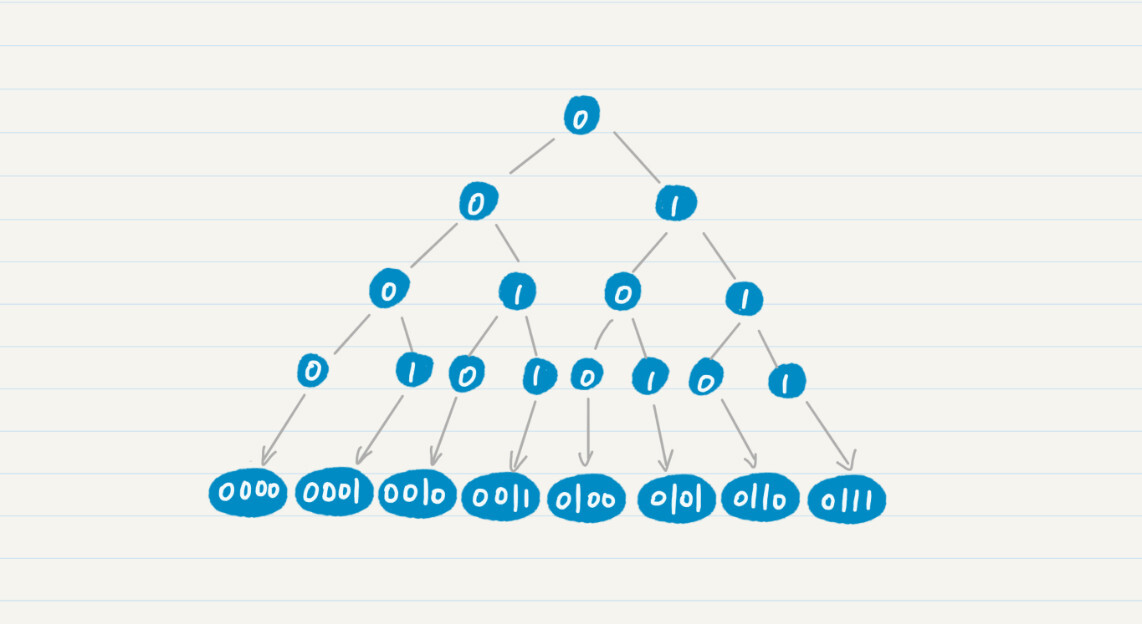
既然树是如此重要，那么我们该如何高效率地访问树中的结点呢？下一讲，我会继续前缀树的话题，讨论如何遍历树中所有结点。

思考题

现在给你一个字典，请尝试实现其前缀树，包括树的构建和查询两个过程。这里，字典可以用字符串数组来表示，每个字符串代表一个单词。

欢迎在留言区交作业，并写下你今天的学习笔记。你可以点击“请朋友读”，把今天的内容分享给你的好友，和他一起精进。

精选留言（15）

• Healtheon 👍（49） 💬（2）

  老师讲解得非常好，谈下个人对前缀树的了解，前缀树主要应用于以下场景： 1.预测文本输入功能：搜索引擎的输入框中输入搜索关键词的预测文本提示、IDE代码编辑器和浏览器网址中输入时的预测文本提示，借助老师讲的前两节动态规划实现预测文本的纠错功能； 2.使用前缀树结构对字符串或单词按字母顺序实现排序并进行输出的功能； 3.前缀树也可用于实现近似匹配，包括拼写检查和连字软件使用的算法； 前缀树的主要优劣对比： 1.使用前缀树可以高效地进行前缀搜索字符串和插入字符串，时间复杂度为O(length)； 2.使用前缀树可以按字母顺序轻松打印所有字符串，该功能是散列表不易实现的，但前缀树的搜索效率可能不如散列表快； 3.前缀树的缺点在于，需要大量的内存来存储字符串，对于每个节点需要太多的节点指针。倘若关注内存空间上的优化，可以考虑使用三元搜索树。三元搜索树是实现字典的首选结构，其搜索字符串的时间复杂度是O(height)；

  2019-01-07


• Healtheon 👍（25） 💬（1）

  下面是构建前缀树和查询的代码实现： package com.string.test; /** * Created by hanyonglu on 2019/1/7. */ public class TrieTest { private static final int CHARACTER_SIZE = 26; private TrieNode root; private static class TrieNode { private TrieNode[] children; private boolean isWordEnd; public TrieNode() { isWordEnd = false; children = new TrieNode[CHARACTER_SIZE]; for (int index = 0; index < CHARACTER_SIZE; index++) { children[index] = null; } } } public void insert(String key) { TrieNode newNode = root; int index; for (int i = 0; i < key.length(); i++) { index = key.charAt(i) - 'a'; if (newNode.children[index] == null) { newNode.children[index] = new TrieNode(); } newNode = newNode.children[index]; } newNode.isWordEnd = true; } public boolean search(String key) { TrieNode searchNode = root; int index; for (int i = 0; i < key.length(); i++) { index = key.charAt(i) - 'a'; if (searchNode.children[index] == null) { return false; } searchNode = searchNode.children[index]; } return (searchNode != null && searchNode.isWordEnd); } public static void main(String args[]) { String[] keys = {"my", "name", "is", "hanyonglu", "the", "son", "handongyang", "home", "near", "not", "their"}; TrieTest trieTest = new TrieTest(); trieTest.root = new TrieNode(); for (int index = 0; index < keys.length ; index++) { trieTest.insert(keys[index]); } System.out.println("home result : " + trieTest.search("home")); System.out.println("their result : " + trieTest.search("their")); System.out.println("t result : " + trieTest.search("t")); } }

  2019-01-07


• Being 👍（5） 💬（1）

  关于思考题的一点想法：其实可以将单词以及字母抽象出来，利用组合模式，形成树形关系，实现递归调用。

  2019-01-07


• 梦倚栏杆 👍（3） 💬（1）

  对于二叉树而言，深度优先遍历是不是就是二叉树的先序遍历啊

  2019-03-26


• Cutler 👍（1） 💬（1）

  正好最近刷到了leetcode上一道关于trie树的题 ## Algorithm ### 1. 题目

  208. 实现 Trie (前缀树) 
  

  ### 2. 题目描述

  实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作。
  
  示例:
  
  Trie trie = new Trie();
  
  trie.insert("apple");
  trie.search("apple");   // 返回 true
  trie.search("app");     // 返回 false
  trie.startsWith("app"); // 返回 true
  trie.insert("app");   
  trie.search("app");     // 返回 true
  说明:
  
  你可以假设所有的输入都是由小写字母 a-z 构成的。
  保证所有输入均为非空字符串。
  

  ### 3. 解答：

  type Trie struct {
      data  byte
      child []*Trie
      isEnd bool
  }
  
  /** Initialize your data structure here. */
  func Constructor() Trie {
      return Trie{
          data:  '/',
          child: make([]*Trie, 26, 26),
          isEnd: false,
      }
  }
  
  func newTrie(data byte) *Trie {
      return &Trie{
          data:  data,
          child: make([]*Trie, 26, 26),
      }
  }
  
  /** Inserts a word into the trie. */
  func (t *Trie) Insert(word string) {
      p := t
      for _, c := range word {
          index := c - 'a'
          if p.child[index] == nil {
              p.child[index] = newTrie(byte(c))
          }
          p = p.child[index]
      }
      p.isEnd = true
  }
  
  /** Returns if the word is in the trie. */
  func (t *Trie) Search(word string) bool {
      p := t
      for _, c := range word {
          index := c - 'a'
          if p.child[index] == nil {
              return false
          }
          p = p.child[index]
      }
      if !p.isEnd {
  
          return false
      } else {
          return true
      }
  }
  
  /** Returns if there is any word in the trie that starts with the given prefix. */
  func (t *Trie) StartsWith(prefix string) bool {
      p := t
      for _, c := range prefix {
          index := c - 'a'
          if p.child[index] == nil {
              return false
          }
          p = p.child[index]
      }
      return true
  }
  

  ### 4. 说明 1. 定义Trie的结构中包含的child 2. child数组用26个英文字符表示，用字符减去`a`就得到数组中的索引
  2020-11-07


• 是我 👍（1） 💬（2）

  觉得二叉树跟正则表达式好像

  2019-05-16


• 崔晓乐 👍（0） 💬（1）

  这里的简单回路，其实就是指，除了第一个结点和最后一个结点相同外，其余结点不重复出现的回路？ 这句话怎么理解呢？ 其余结点不重复出现的回路？

  2021-09-14


• 张祈璟 👍（0） 💬（1）

  把词都放在个数据库里，查询的时候用like，与把词放树里的效率哪个高？实现起来哪个简单？

  2021-06-10


• 北极的大企鹅 👍（0） 💬（1）

  讲得非常好

  2021-04-12


• aoe 👍（0） 💬（1）

  这次通俗易懂，感谢老师

  2019-12-02


• Eleven 👍（0） 💬（1）

  老师，这篇概念有点多啊，文章中说的有向边该怎么理解呢？

  2019-11-25


• 花指令 👍（0） 💬（1）

  发现大家用循环遍历确定节点，既然是字母，大小写最多就52个，那应该用ascii做二分搜索更快，分布均匀的话还可以直接用数组下标

  2019-11-04


• Better me 👍（0） 💬（1）

  想问下老师最后小结中对应的左子树为0右子树为1对应的二进制数有什么实际应用场景吗

  2019-07-28


• pyhhou 👍（0） 💬（1）

  简单实现了下，跑了几个例子是可以work的，这里build的时候用Map是考虑到字典里面的单词和解释以key-value的形式出现，search函数输入是单词输出是解释，没有该单词的话返回null public class Trie { private class TrieNode { private TrieNode[] children = new TrieNode[26]; private String word = null; private String explanation = null; } private TrieNode root = new TrieNode(); public void buildTrie(Map<String, String> dictionary) { if (dictionary == null || dictionary.size() == 0) { return; } for (String word : dictionary.keySet()) { char[] wordArr = word.toCharArray(); TrieNode tmp = root; for (char c : wordArr) { if (tmp.children[c - 'a'] == null) { tmp.children[c - 'a'] = new TrieNode(); } tmp = tmp.children[c - 'a']; } tmp.word = word; tmp.explanation = dictionary.get(word); } } public String searchTrie(String targetWord) { if (targetWord == null || targetWord.isEmpty()) { return null; } char[] targetWordArr = targetWord.toCharArray(); TrieNode tmp = root; for (char c : targetWordArr) { if (tmp.children[c - 'a'] == null) { return null; } tmp = tmp.children[c - 'a']; } return tmp.explanation; }

  2019-01-18


• 李尧 👍（0） 💬（1）

  老师好，根节点的高度可以随意设置吗，假如设置为1，子节点的高度是不是都需要加1

  2019-01-07