09 动态规划(上):如何实现基于编辑距离的查询推荐?
你好,我是黄申。
上一篇讲组合的时候,我最后提到了有关文本的关键字查询。今天我接着文本搜索的话题,来聊聊查询推荐(Query Suggestion)的实现过程,以及它所使用的数学思想,动态规划(Dynamic Programming)。
那什么是动态规划呢?在递归那一节,我说过,我们可以通过不断分解问题,将复杂的任务简化为最基本的小问题,比如基于递归实现的归并排序、排列和组合等。不过有时候,我们并不用处理所有可能的情况,只要找到满足条件的最优解就行了。在这种情况下,我们需要在各种可能的局部解中,找出那些可能达到最优的局部解,而放弃其他的局部解。这个寻找最优解的过程其实就是动态规划。
动态规划需要通过子问题的最优解,推导出最终问题的最优解,因此这种方法特别注重子问题之间的转移关系。我们通常把这些子问题之间的转移称为状态转移,并把用于刻画这些状态转移的表达式称为状态转移方程。很显然,找到合适的状态转移方程,是动态规划的关键。
因此,这两节我会通过实际的案例,给你详细解释如何使用动态规划法寻找最优解,包括如何分解问题、发现状态转移的规律,以及定义状态转移方程。
编辑距离
当你在搜索引擎的搜索框中输入单词的时候,有没有发现,搜索引擎会返回一系列相关的关键词,方便你直接点击。甚至,当你某个单词输入有误的时候,搜索引擎依旧会返回正确的搜索结果。
搜索下拉提示和关键词纠错,这两个功能其实就是查询推荐。查询推荐的核心思想其实就是,对于用户的输入,查找相似的关键词并进行返回。而测量拉丁文的文本相似度,最常用的指标是编辑距离(Edit Distance)。
我刚才说了,查询推荐的这两个功能是针对输入有缺失或者有错误的字符串,依旧返回相应的结果。那么,将错误的字符串转成正确的,以此来返回查询结果,这个过程究竟是怎么进行的呢?
由一个字符串转成另一个字符串所需的最少编辑操作次数,我们就叫作编辑距离。这个概念是俄罗斯科学家莱文斯坦提出来的,所以我们也把编辑距离称作莱文斯坦距离(Levenshtein distance)。很显然,编辑距离越小,说明这两个字符串越相似,可以互相作为查询推荐。编辑操作有这三种:把一个字符替换成另一个字符;插入一个字符;删除一个字符。
比如,我们想把mouuse转换成mouse,有很多方法可以实现,但是很显然,直接删除一个“u”是最简单的,所以这两者的编辑距离就是1。
状态转移
对于mouse和mouuse的例子,我们肉眼很快就能观察出来,编辑距离是1。但是我们现实的场景中,常常不会这么简单。如果给定任意两个非常复杂的字符串,如何高效地计算出它们之间的编辑距离呢?
我们之前讲过排列和组合。我们先试试用排列的思想来进行编辑操作。比如,把一个字符替换成另一个字符,我们可以想成把A中的一个字符替换成B中的一个字符。假设B中有m个不同的字符,那么替换的时候就有m种可能性。对于插入一个字符,我们可以想成在A中插入来自B的一个字符,同样假设B中有m个不同的字符,那么也有m种可能性。至于删除一个字符,我们可以想成在A中删除任何一个字符,假设A有n个不同的字符,那么有n种可能性。
可是,等到实现的时候,你会发现实际情况比想象中复杂得多。
首先,计算量非常大。我们假设字符串A的长度是n,而B字符串中不同的字符数量是m,那么A所有可能的排列大致在m^n这个数量级,这会导致非常久的处理时间。对于查询推荐等实时性的服务而言,服务器的响应时间太长,用户肯定无法接受。
其次,如果需要在字符串A中加字符,那么加几个呢,加在哪里呢?同样,删除字符也是如此。因此,可能的排列其实远不止m^n。
我们现在回到问题本身,其实编辑距离只需要求最小的操作次数,并不要求列出所有的可能。而且排列过程非常容易出错,还会浪费大量计算资源。看来,排列的方法并不可行。
好,这里再来思考一下,其实我们并不需要排列的所有可能性,而只是关心最优解,也就是最短距离。那么,我们能不能每次都选择出一个到目前为止的最优解,并且只保留这种最优解?如果是这样,我们虽然还是使用迭代或者递归编程来实现,但效率上就可以提升很多。
我们先考虑最简单的情况。假设字符串A和B都是空字符串,那么很明显这个时候编辑距离就是0。如果A增加一个字符a1,B保持不动,编辑距离就增加1。同样,如果B增加一个字符b1,A保持不动,编辑距离增加1。但是,如果A和B有一个字符,那么问题就有点复杂了,我们可以细分为以下几种情况。
我们先来看插入字符的情况。A字符串是a1的时候,B空串增加一个字符变为b1;或者B字符串为b1的时候,A空串增加一个字符变为a1。很明显,这种情况下,编辑距离都要增加1。
我们再来看替换字符的情况。当A和B都是空串的时候,同时增加一个字符。如果要加入的字符a1和b1不相等,表示A和B之间转化的时候需要替换字符,那么编辑距离就是加1;如果a1和b1相等,无需替换,那么编辑距离不变。
最后,我们取上述三种情况中编辑距离的最小值作为当前的编辑距离。注意,这里我们只需要保留这个最小的值,而舍弃其他更大的值。这是为什么呢?因为编辑距离随着字符串的增长,是单调递增的。所以,要求最终的最小值,必须要保证对于每个子串,都取得了最小值。有了这点,之后我们就可以使用迭代的方式,一步步推导下去,直到两个字符串结束比较。
刚才我说的情况中没有删除,这是因为删除就是插入的逆操作。如果我们从完整的字符串A或者B开始,而不是从空串开始,这就是删除操作了。
从上述的过程可以看出,我们确实可以把求编辑距离这个复杂的问题,划分为更多更小的子问题。而且,更为重要的一点是,我们在每一个子问题中,都只需要保留一个最优解。之后的问题求解,只依赖这个最优值。这种求编辑距离的方法就是动态规划,而这些子问题在动态规划中被称为不同的状态。
如果文字描述不是很清楚的话,我这里又画一张表,把各个状态之间的转移都标示清楚,你就一目了然了。
我还是用mouuse和mouse的例子。我把mouuse的字符数组作为表格的行,每一行表示其中一个字母,而mouse的字符数组作为列,每列表示其中一个字母,这样就得到下面这个表格。

这张表格里的不同状态之间的转移,就是状态转移。其中红色部分表示字符串演变(或者说状态转移)的方式以及相应的编辑距离计算。对于表格中其他空白的部分,我暂时不给出,你可以试着自己来推导。
编辑距离是具有对称性的,也就是说从字符串A到B的编辑距离,和从字符串B到A的编辑距离,两者一定是相等的。这个应该很好理解。
你可以把刚才那个状态转移表的行和列互换一下,再推导一下,看看得出的编辑距离是否还是1。我现在从理论上解释下这一点。这其实是由编辑距离的三种操作决定的。比如说,从字符串A演变到B的每一种操作,都可以转换为从字符串B演变到A的某一种操作。
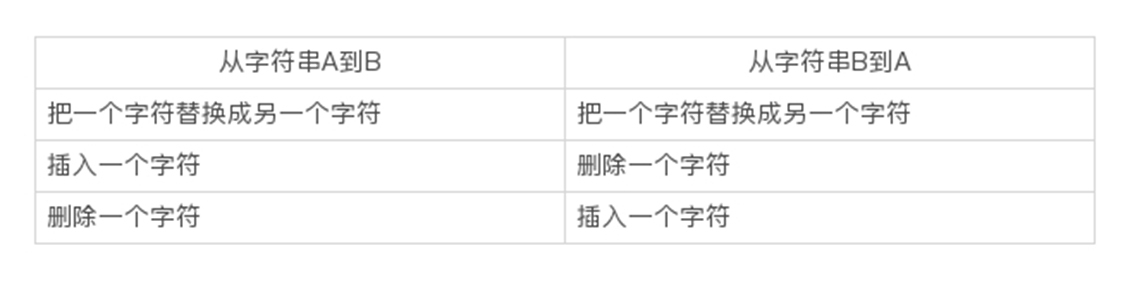
所以说,从字符串A演变到B的每一种变化方式,都可以找到对应的从字符串B演变到A的某种方式,两者的操作次数一样。自然,代表最小操作次数的编辑距离也就一样了。
小结
我今天介绍了用于查询推荐的编辑距离。编辑距离的定义很好理解,不过,求任意两个字符串之间的编辑距离可不是一件容易的事情。我先尝试用排列来分析问题,发现这条路走不通,而后我们仍然使用了化繁为简的思路,把编辑距离的计算拆分为3种情况,并建立了子串之间的联系。
你不要觉得这样的分析过程比较繁琐,我想说的是,学数学固然是为了得到结果,但是学习的过程,是要学会解决问题的方法和思路。比如面对一个问题的时候,你可能不知道用什么方法来解决,但是你可以尝试用我们学过的这些基础思想去分析,去比对,在这个分析的过程中去总结这些方法的使用规律,久而久之,你就能摸索出自己解决问题的套路。
比如说,动态规划虽然也采用了把问题逐步简化的思想,但是它和基于递归的归并排序、排列组合等解法有所不同。能够使用动态规划解决的问题,通常只关心一个最优解,而这个最优解是单调改变的,例如最大值、最小值等等。因此,动态规划中的每种状态,通常只保留一个当前的最优解,这也是动态规划效率比较高的原因。

思考题
理解了动态规划法和状态转移之后,你觉得根据编辑距离来衡量字符串之间的相似程度有什么局限性?你有什么优化方案吗?
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
- 任鹏斌 👍(53) 💬(3)
关于编辑距离的计算看了好多遍还是不太理解 1、A、B都为空A转化为B或者B转化为A不需要做任何操作编辑距离为0(可以理解) 2、A增加一个字符a1,B保持不动,编辑距离为1。或者B增加一个字符b1,A保持不动,编辑距离为1.(初始为空的情况,可以理解) 3、如何A和B有一个字符那么情况就有点复杂了,具体如下: (1)插入字符的情况,A字符串为a1的时候,B空串增加一个字符变为b1,或者B字符串为b1的时候,A空串增加一个字符变为a1。很明显这种情况下编辑距离都要增加1 问题:这时候如果b1和a1是一样的字符A或者B再插入后已经是一样的了也不需要再做转化了,这时候编辑距离是否应该就是1?下面的表格中A、B串的m与m处的插入情况与这里一样插入的编辑距离为什么是2? (2)替换字符的情况,可以理解为不相等的情况下才替换所以此时编辑距离加1,如果相等不需要替换则编辑距离为0? 麻烦老师解答一下,谢谢!
2019-01-07 - 西北偏北 👍(15) 💬(2)
搜索引擎中的自动纠错和提示功能,是对用户输入字符串,计算其相似字符串。 比如mouse就是用户输入mouuse的相似字符串。 一个字符串有哪些相似字符串,无非是把该字符串进行一系列可能的变形编辑。比如把某个字母删掉,或增加一个字母,或替换该字母 最后看变形后的单词,是否是一个合法单词。如果是,则给用户提示。 原始单词或字符变形到一个合法字符串的步数,称为这两个单词之间的编辑距离。 但一个单词随着长度增加,其对应的合法单词,编辑距离计算将会很多。不可取。 所以需要最优解,找出用户输入词,编辑距离最小的目标词即可
2019-01-15 - somenzz 👍(9) 💬(1)
有时候编辑距离最短的字符串并不能代表用户真正想输入的正确字符串,例如用户输出了 worder,实际上是想查 worker,但编辑距离为 1 的有很多,如 warder,wonder,我在想是不是应该按用户输入的字符串前辍最一致的字符串开始再计算编辑距离,例子中的 mouuse 和 mouse ,先直接替换掉前面一样的 mou,直接计算 use 和 se 的编辑距离,再从替换后面一样的 se,这样就是直接计算 u 和空串的编辑距离,这样就可以很快计算出距离为1,不知道这样理解优化是否正确,请老师指点。
2019-01-06 - 凡间的雨 👍(7) 💬(3)
https://www.jianshu.com/p/4678d3f7b6f1 之前写过的一篇编辑距离文章,代码是用动态规划的方式实现的。
2020-04-13 - Jerry银银 👍(6) 💬(1)
老师,如果让您给计算机相关的职场人推荐一本关于数学的书,您会推荐什么?
2019-01-08 - Yang 👍(5) 💬(1)
编辑距离没办法刻画语义信息,比如同义词,否定词(编辑距离很短)。
2019-10-09 - danvid 👍(4) 💬(3)
编辑距离解析,其实看看下面这个结合图会好理解一点,其实就是下一个结果基于上一个结果的一种情况去进行加0还是加0,老师说的真的一头雾水,大家可以参考一下 解析: i相当于第几行,j相当于第几列 1.如果i或者j=0就是edit(i,j)=j或者i; 2.左(i-1,j),上(i,j-1),左上(i-1,j-1)相当于前一个子集可能出现的三种情况的下求最小值,其中左+1,上+1,右上(如果当前i=j,则+0,不等则+1),,求这三者的最小值例如:左=1,左上=0,上=1则 edit(左)=1+1=2,如果当前格子对应行列的数据相等则edit(左上)=0+0=0,否则edit(左上)=0+1=1,edit(上)=1+1=2,所以结果就是edit(i,j)=min{edit(左),edit(左上),edit(上)}
2019-05-16 - 书木子谢明 👍(3) 💬(1)
向老师请教几个问题: 1.适应动态规划的要求是 sum(每一步最优解)=最终最优解,这样的理解对吗?应该有问题不适合动态规划求解,如何辨别呢? 2. 我理解的“编辑的最短距离”描述的是两个字符串相似性的一种方式,这种方式需要逐个迭代字符,在英文环境中该算法可以推荐到单词级别,中文环境貌似只能推荐到词级别。ES中计算搜索结果相似程度也是用的“编辑距离”么?
2019-07-17 - 等待 👍(2) 💬(1)
首先,计算量非常大。我们假设字符串 A 的长度是 n,而 B 字符串中不同的字符数量是 m,那么 A 所有可能的排列大致在 m^n 这个数量级。 这里的m^n是如何得知的呢?这个没看懂,谢谢
2020-06-15 - 伊利丹怒风 👍(2) 💬(1)
其实例子的三种操作是对应状态转移表里面分别从:上、左、左上(斜线)变换过来的三种可能性。按这个理解会更容易一些,比如第一个A:m、B:m的理解: 1、从“左”过来:A:m,B:0,由于B:0->m,所以需要增加一个“插入”操作,也就是1+1=2 2、从“上”转移过来:A:0,B:m,由于A:0->m,所以需要增加一个“删除”操作,也就是1+1=2 3、从“左上”转移过来:A:0,B:0,由于A,B都增加了一个字符,所以需要增加一个“替换”操作,由于这里A、B增加的字符相等,所以无需“替换”,因此0+0 = 0
2020-02-20 - caohuan 👍(2) 💬(1)
本篇所得:动态规划 为寻找的最优解,它只关心 最优的一个解,其他的不会再考虑,比如求解 数组的最大 和最小值,一般只有一个(可能有重复的最值,但最值是相等的)。 工作和生活中,我们一般把大问题分解为小问题,再把小问题 分解为容易解答的问题,动态规划 就是在 容易解答的问题中选择最优解。 黄老师 在文中提到:搜索引擎输入的搜索词的查询和推荐,就是对 缺失和错误的字符串进行操作,比如我们输入错误的字符串A,和正确的字符串B,需要把字符串A改到B,需要把字符串 分解到字符 的小问题,然后进行‘增、删、改’等操作,这里运用 动态规划 寻找最优解,不需要使用排列 这么复杂的方法 因为排列计算消耗的时间会很长,运用动态规划 很节能。 今天所得:解决问题的方法 (1)不断的分解问题,把大问题分解为小问题,把小问题 再分解...直至到可以解答的问题;(2)使用动态规划 求解 小问题的 最优解。 回答老师的问题:用编辑距离对字符串状态转移资源消耗的标记,会浪费很多 内存和运算资源,可以把 字符串 再分割成字符,把 二个字符串的不同的字符 掏出来,再用编辑距离 处理,应该会更快一下、占用资源也少一些,老师是否同意,也期待 黄老师的指正。 老师 可以用 斐波那契数列 来说明 动态规划的问题,更让我们易理解。
2019-01-21 - 菩提 👍(2) 💬(1)
老师,表格中插入一个字符m,编辑距离增加1。为什么说整体编辑距离是2呢? 如果推导表格往下移动一格,字符串A变成mo,字符串B变成了m,这时应该如何推导啊?希望您帮忙解答一下,第一次实际接触动态规划,谢谢! 最近反复看这两篇动态规划,表格推导看的有点似懂非懂。望老师指导一下
2019-01-06 - 惜心(伟祺) 👍(1) 💬(1)
局部最优 做不到全局最优
2020-12-09 - 阳仔 👍(1) 💬(1)
动态规划要理解状态转移方程是“动态”的。 通过上一次的状态来推导本次状态,而本次可以通过不同的上一次状态来推导, 例如某个上一次状态编辑操作数是2,而本次编辑操作次数需要1,那么从该上一次状态到本次状态的操作数就是2+1=3,主要关注状态的转移带来的变化。 最后根据具体问题取其中的最优解
2020-06-24 - 建强 👍(1) 💬(1)
如果词库中的词条数量很大,利用编辑距离来匹配词条的相似度效率会比较低,因为编辑距离的计算是逐个字符进行匹配扫描的,做相似度匹配时需要选出编辑距离最短的那个词条,这样就需要扫描整个词库,才能获得具有最短距离的词条。 我个人的优化方案:预先把每个词条的前缀全部剥离出来,某些词条的前缀可能是重复的,建立前缀与词条的一对多关系,利用哈希算法,得到每个前缀的哈希值,同时把各个前缀存贮于哈希表中,哈希表中除了存贮前缀哈希值,同时还存贮该前缀属于哪个词条,即词条的索引号,这样每次查询时,先把要查询的词条按相同的哈希算法,算出哈希值,再根据哈希值,得到该前缀所属的所有词条,这样就缩小了查询范围,然后再计算每个词条和被查询的词条的编辑距离,得到相近的词。 以上是我个人的一点浮浅理解,请老师指正。
2019-11-02