数学专栏课外加餐(一) 我们为什么需要反码和补码?
你好,我是黄申。欢迎来到第一次课外加餐时间。
专栏已经更新了几讲,看到这么多人在留言区写下自己的疑惑和观点,我非常开心。很多同学在留言里提出了很多非常好的问题,所以我决定每隔一段时间,对留言里的疑问、有代表性的问题做个集中的解答,也是对我们主线内容做一个补充,希望对你有帮助。
什么是符号位?为什么要有符号位?
在第1讲里,我介绍了十进制数转二进制数。这里面很多人对逻辑右移和算术右移中提到的符号位和补码有疑惑。这里面涉及了几个重要的概念,包括符号位、溢出、原码、反码和补码。我详细讲一下这几个点的来龙去脉。
首先我们来看,什么是符号位,为什么要有符号位?用一句话来概括就是,符号位是有符号二进制数中的最高位,我们需要它来表示负数。
在实际的硬件系统中,计算机CPU的运算器只实现了加法器,而没有实现减法器。那么计算机如何做减法呢?我们可以通过加上一个负数来达到这个目的。比如,3-2可以看作3+(-2)。因此,负数的表示对于计算机中的二进制减法至关重要。
那么,接下来的问题就是,如何让计算机理解哪些是正数,哪些是负数呢?为此,人们把二进制数分为有符号数(signed)和无符号数(unsigned)。
如果是有符号数,那么最高位就是符号位。当符号位为0时,表示该数值为正数;当符号位为1时,表示该数值为负数。例如一个8位的有符号位二进制数10100010,最高位是1,这就表示它是一个负数。
如果是无符号数,那么最高位就不是符号位,而是二进制数字的一部分,例如一个8位的无符号位二进制数10100010,我们可以通过第1讲讲过的内容,换算出它所对应的十进制数是162。由于没有表示负数的符号位,所有无符号位的二进制都代表正数。
有些编程语言,比如Java,它所有和数字相关的数据类型都是有符号位的;而有些编程语言,比如C语言,它有诸如unsigned int这种无符号位的数据类型。
下面我们来看,什么是溢出?
在数学的理论中,数字可以有无穷大,也有无穷小。可是,现实中的计算机系统,总有一个物理上的极限(比如说晶体管的大小和数量),因此不可能表示无穷大或者无穷小的数字。对计算机而言,无论是何种数据类型,都有一个上限和下限。
在Java中,int型是32位,它的最大值也就是上限是231-1(最高位是符号位,所以是2的31次方而不是32次方),最小值也就是下限是-231。而long型是64位,它的最大值,也就是上限是263-1;最小值,也就是下限是-263。
对于n位的数字类型,符号位是1,后面n-1位全是0,我们把这种情形表示为-2^(n-1) ,而不是2^(n-1)。一旦某个数字超过了这些限定,就会发生溢出。如果超出上限,就叫上溢出(overflow)。如果超出了下限,就叫下溢出(underflow)。
那么溢出之后会发生什么呢?我以上溢出为例来给你解释。
n位数字的最大的正值,其符号位为0,剩下的n-1位都为1,再增大一个就变为了符号位为1,剩下的n-1位都为0。而符号位是1,后面n-1位全是0,我们已经说过这表示-2^(n-1)。
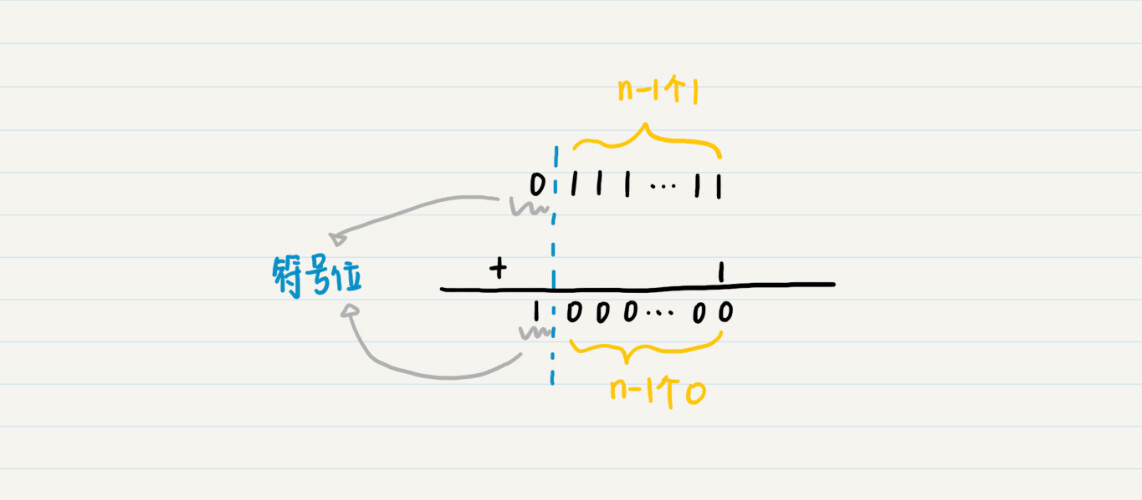
那么就是说,上溢出之后,又从下限开始,最大的数值加1,就变成了最小的数值,周而复始,这不就是余数和取模的概念吗?下面这个图可以帮助你理解。
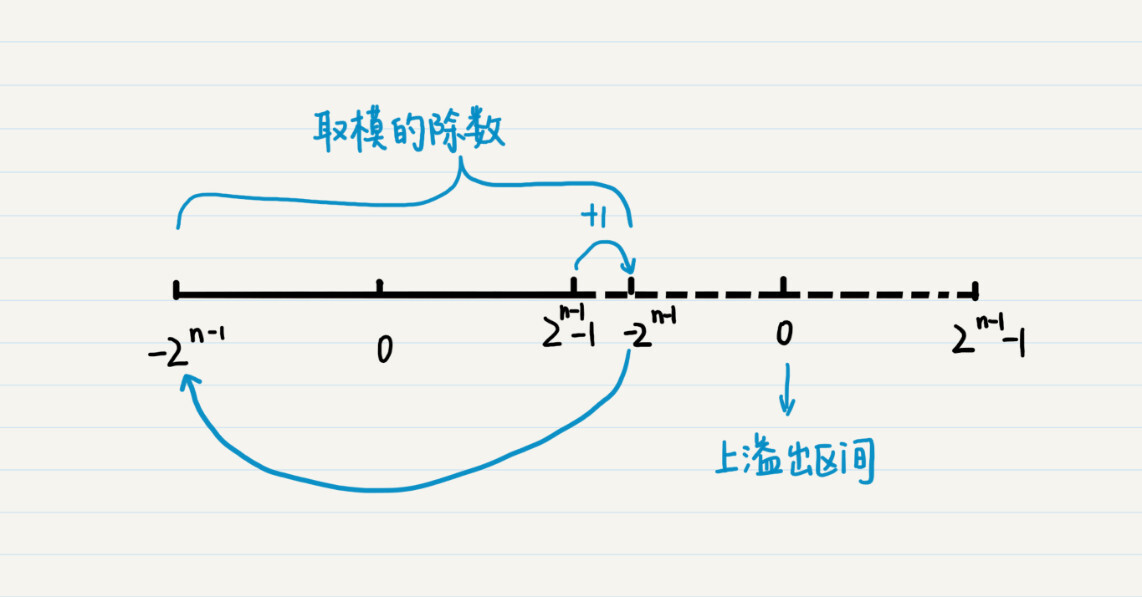
其中右半部分的虚线表示已经溢出的区间,而为了方便你理解,我将溢出后所对应的数字也标在了虚线的区间里。由此可以看到,所以说,计算机数据的溢出,就相当于取模。而用于取模的除数就是数据类型的上限减去下限的值,再加上1,也就是(2(n-1)-1)-(-2(n-1))+1=2x2(n-1)-1+1=2n-1+1。
你可能会好奇,这个除数为什么不直接写成2n呢?这是因为2n已经是n+1位了,已经超出了n位所能表示的范围。
二进制的原码、反码及补码
理解了符号位和溢出,我接下来说说,什么是二进制的原码、反码和补码,以及我们为什么需要它们。
原码就是我们看到的二进制的原始表示。对于有符号的二进制来说,原码的最高位是符号位,而其余的位用来表示该数字绝对值的二进制。所以+2的原码是000…010,-2的的原码是100.…010。
那么我们是不是可以直接使用负数的原码来进行减法计算呢?答案是否定的。我还是以3+(-2)为例。
假设我们使用Java中的32位整型来表示2,它的二进制是000…010。最低的两位是10,前面的高位都是0。如果我们使用-2的原码,也就是100…010,然后我们把3的二进制原码000…011和-2的二进制原码100…010相加,会得到100…0101。具体计算你可以看我画的这张图。
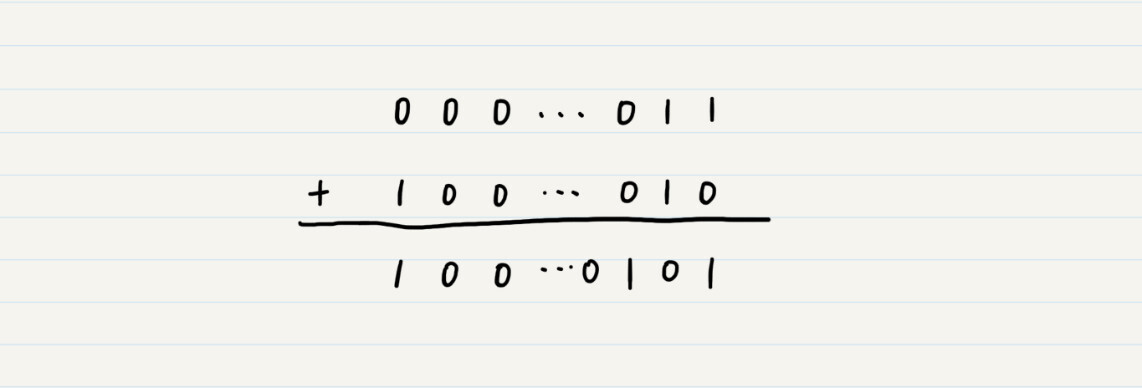
二进制编码上的加减法和十进制类似,只不过,在加法中,十进制是满10才进一位,二进制加法中只要满2就进位;同样,在减法中,二进制借位后相当于2而不是10。
相加后的结果是二进制100…0101,它的最高位是1,表示负数,而最低的3位是101,表示5,所以结果就是-5的原码了,而3+(-2)应该等于1,两者不符。
如果负数的原码并不适用于减法操作,那该怎么办呢?这个问题的解答还要依赖计算机的溢出机制。
我刚刚介绍了溢出以及取模的特性,我们可以充分利用这一点,对计算机里的减法进行变换。假设有i-j,其中j为正数。如果i-j加上取模的除数,那么会形成溢出,并正好能够获得我们想要的i-j的运算结果。如果我说的还是不太好理解,你可以参考下面这张图。
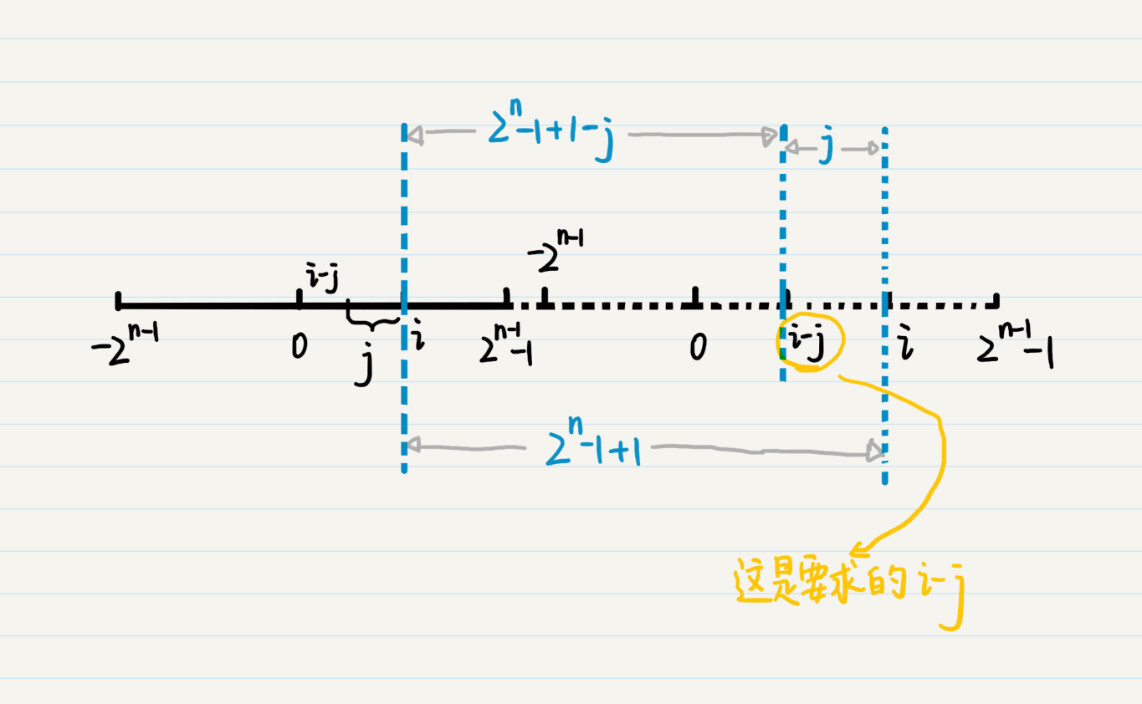
我们把这个过程用表达式写出来就是i-j=(i-j)+(2n-1+1)=i+(2n-1-j+1)。
其中2n-1的二进制码在不考虑符号位的情况下是n-1位的1,那么2n-1-2的结果就是下面这样的:
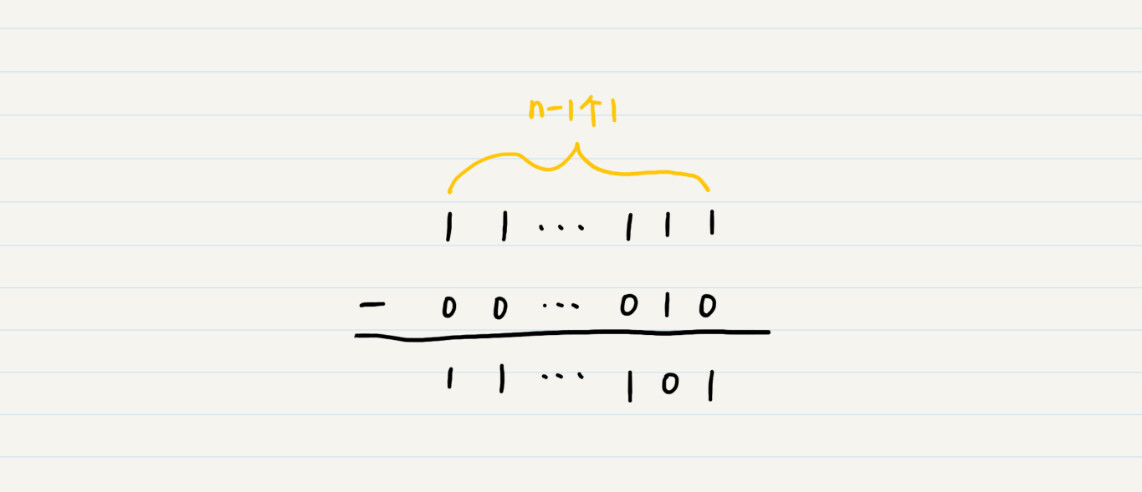
从结果可以观察出来,所谓2n-1-j相当于对正数j的二进制原码,除了符号位之外按位取反(0变1,1变0)。由于负数-j和正数j的原码,除了符号位之外都是相同的,所以,2n-1-j也相当于对负数-j的二进制原码,除了符号位之外按位取反。我们把2^n-1-j所对应的编码称为负数-j的反码。所以,-2的反码就是1111…1101。
有了反码的定义,那么就可以得出i-j=i+(2^n-1-j+1)=i的原码+(-j的反码)+1。
如果我们把-j的反码加上1定义为-j的补码,就可以得到i-j=i的原码+(-j的补码)。
由于正数的加法无需负数的加法这样的变换,因此正数的原码、反码和补码三者都是一样的。最终,我们可以得到i-j=i的补码+(-j的补码)。
换句话说,计算机可以通过补码,正确地运算二进制减法。我们再来用3+(-2)来验证一下。正数3的补码仍然是0000…0011,-2的补码是1111…1110,两者相加,最后得到了正确的结果1的二进制。
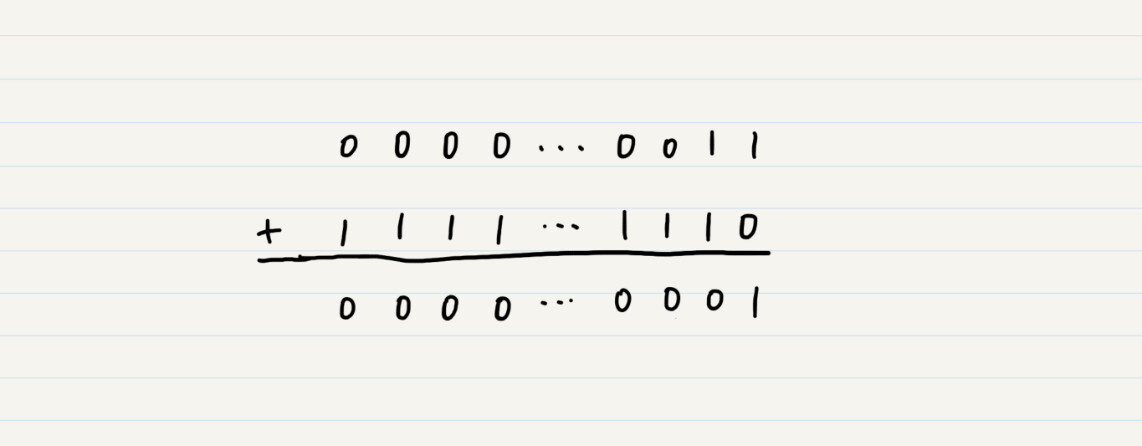
可见,溢出本来是计算机数据类型的一种局限性,但在负数的加法上,它倒是可以帮我们大忙。
最后,给你留一道思考题吧。理解了负数的原码、反码和补码之后,你能算算看,8位的有符号位二进制数10100010,对应的是哪个十进制数吗?
好了,关于二进制的补充内容就到这里了。欢迎你继续留言给我。你也可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
- 奔跑的蜗牛 👍(5) 💬(1)
疑问1:为什么i-j得加上取模的除数? 疑问2:2^n-1就是32位1,这个地方就又没有符号位之说了? 疑问3:非符号位计算溢出会进到符号位嘛? 麻烦老师帮忙解答下
2019-04-27 - 梓航(﹏) 👍(31) 💬(1)
老师,你讲的那个取模和反码的关系那一段我看不懂,之前看书也没有遇到你说的这种概念,请问还有其他学习资料吗?
2018-12-24 - 随欣所遇 👍(22) 💬(2)
用大家熟悉的一周七天进行对比吧 1、计算数据的溢出相当于模:假设第1天为周一,第2天为周二,以此类推第7天为周日,第8天已经大于7溢出了,8对7进行取模为1,也即第八天为周一;取模的除数为上限减去下限+1,替换过来换算:一周的上限为7,下限为1,那一周取模的除数换算为:7-1+1,所以我们想要知道第15天后是周几直接对(7-1+1)取模即可; 2、i-j=(i-j)+(2^n-1+1)=i+(2^n-1-j),可以换算为 周一 = (周一)+ (7-1+1)进行理解(ps:不一定周一,周几都为同一样,只是将 i-j 看成一个单元用其做概念上的替换)
2019-04-12 - 石佳佳_Gemtra 👍(19) 💬(4)
思考题: 原码:10100010 对补码除符号位取反得 反码:11011101 +1操作得 补码:11011110 对应十进制数:-94 还有一种方法,把负数原码除符号位外求和,减去 (2^n-1+1),即 2+32-(2^7-1+1)=-94
2018-12-24 - 风轨 👍(12) 💬(1)
思考题 0b10100010 = 0b10000000 + 0b00100010 其中 0b10000000 = -128 0b00100010 = 34 所以答案是 -94 2进制取相反数公式 相反数 = 原数减一再取反 - 0b10100010 = !(0b10100010-1) = 0b01011110 = 94
2018-12-24 - 恒 👍(7) 💬(1)
补码代码的数值的快速求法 负数补码通过非符号位0出现的位置来计算,然后计算结果加1,最后带上符号即可。 比如 1000,非符号位为000,按照0出现的位置计算,000=2^2+2^1+2^0=4+2+1=7,结果加上1后得到8,所以这个二进制数 表示-8 正数补码看非符号位1出现的位置来计算,然后加上符号即可。 比如 0111,非符号位为111,按照1出现的位置计算,111=4+2+1=7 所以这个二进制数 表示+7 对补码的理解: 目的:为了使用相同电路来实现加减运算,使得计算机cpu设计更加容易 为何用补码,可以通过如下四位数模拟补码从0开始一直加1的情况 0000 = 0 0001 = 1 0010 = 2 0011 = 3 0100 = 4 0101 = 5 0110 = 6 0111 = 7 1000 = -8 1001 = -7 1010 = -6 1011 = -5 1100 = -4 1101 = -3 1110 = -2 1111 = -1 0000 = 0 (再加1又从0开始了,上面表示的不同数值的个数是2^4=16,所以模是16) ... 然后上溢和下溢也顺便理解了,如下所示, 上溢就是4位二进制数的正数的最大值加1,然后通过补码加法运算后结果是4位二进制数的最小数-8 上溢:7 + 1 =0111+0001=1000(4位二进制数的最小数)=-8 注:加上1的目的是最大值再大一点,当然就溢出了 下溢就是4位二进制数的负数的最小值加-1,然后通过补码加法运算后结果是4位二进制数的最大数+7 下溢:-8+(-1)=1000+1111=0111(最大数)=7 注:加上-1的目的是最小值再小一点,当然就溢出了
2019-06-18 - Temme 👍(6) 💬(1)
思考题:10100010 如果是原码,所对应的数字就是-34 如果是补码,那么就减一取反求原码,11011110,就是-94。 然而对着补码再去求一次补码也可以得出原码,所以神奇的是某个回答也是对的。。。这就是所谓的互为补码。
2019-06-19 - 彩色的沙漠 👍(6) 💬(1)
老师,不好意思 问题有一处错误,我纠正一下,以免误导后来的同学 java中int的最小值是-2^31 二进制源码:1 000 0000 0000 0000 0000 0000 0000 0000 二进制反码:1 111 1111 1111 1111 1111 1111 1111 1111 -2^31的补码还是自己,符号位进位舍弃
2018-12-26 - 夏飞 👍(5) 💬(1)
这不就是余数和取模的概念吗? 这句话不明其意
2018-12-25 - 爱吃锅巴的沐泡 👍(4) 💬(1)
老师,请教一下问题 文章中讲的是原码到补码的推导过程。 一个二进制数在计算机中存储的形式就是补码。 那么一个数输入到计算机中就是补码形式,还是说有一个从原码到补码的推导过程?可是这个推导过程中也有减法,和补码把减法加法化的说法就冲突了?
2019-06-26 - 吾本糊涂 👍(3) 💬(1)
10100010直接用10进制表示不是-34吗 为啥要去它的补码再换算10进制?
2018-12-25 - 毕明亮 👍(3) 💬(1)
老师,评论里石佳佳说那个是源码取反加一,Li Shundong又说是补码取反加一得源码……看晕了
2018-12-24 - chengzise 👍(3) 💬(1)
计算机内部有符号数才用补码表示,10100010最高位为1是个负数,负数的绝对值是其补码取反再加1,为01011110。十进制为94.因此10100010的十进制值为-94
2018-12-24 - 江宁猎妈人 👍(2) 💬(1)
以前学计算机原理的时候,一直想不明白为啥补码这么设计,虽然也知道是取余,但一直没很清楚的推导过。这次看了文章更有体会。拿 4 位 2 进制数举例,-2 原码 1010,补码 1110,相当于 -6 的原码 ,也就是 -6 = -8 - (-2),而 -8 正是一个循环。给 -6 加 1,1110 + 0001 = 1111 (-7), -7 还原以后就是 - 1 = -2 + 1;继续下去 1111 + 0001 = 1/ 0000 = 0,这样就转回来了。 同样的,这也是补码 1000 代表 -8 的原因。 和上面一样,1001 是 -7 的补码,也是 -1 的原码。再减一位,变成1000 ,若用原码表示法,就是 -0,和 0000 都是 0,浪费了一个数。若以补码的思想,-8 - 0 = -8,这样摇身一变,就使得表示范围多了一位,弥补了 2 ^ n 的边界值。
2020-03-18 - Rainbow 👍(2) 💬(1)
“其中 2^n-1 的二进制码在不考虑符号位的情况下是 n-1位的1“ 这个地方不理解,2^n-1的符号位不是0吗? 而2^n - 1是有位的1啊。 这个地方不理解,希望老师能解答一下~
2018-12-27