16 浮点数和定点数（下）：深入理解浮点数到底有什么用？

上一讲，我们讲了用“浮点数”这样的数据形式，来表示一个不能确定大小的数据范围。浮点数可以大到$3.40×10^{{38}$，也可以小到$1.17×10}$这种形式的，才是一个精确的浮点数。}$这样的数值。同时，我们也发现，其实我们平时写的0.1、0.2并不是精确的数值，只是一个近似值。只有0.5这样，可以表示成$2^{-1

你是不是感到很疑惑，浮点数的近似值究竟是怎么算出来的？浮点数的加法计算又是怎么回事儿？在实践应用中，我们怎么才用好浮点数呢？这一节，我们就一起来看这几个问题。

浮点数的二进制转化

我们首先来看，十进制的浮点数怎么表示成二进制。

我们输入一个任意的十进制浮点数，背后都会对应一个二进制表示。比方说，我们输入了一个十进制浮点数9.1。那么按照之前的讲解，在二进制里面，我们应该把它变成一个“符号位s+指数位e+有效位数f”的组合。第一步，我们要做的，就是把这个数变成二进制。

首先，我们把这个数的整数部分，变成一个二进制。这个我们前面讲二进制的时候已经讲过了。这里的9，换算之后就是1001。

接着，我们把对应的小数部分也换算成二进制。小数怎么换成二进制呢？我们先来定义一下，小数的二进制表示是怎么回事。我们拿0.1001这样一个二进制小数来举例说明。和上面的整数相反，我们把小数点后的每一位，都表示对应的2的-N次方。那么0.1001，转化成十进制就是：

$1×2^{-1}+0×2+0×2^{{-3}+$

$1×2}=0.5625$

和整数的二进制表示采用“除以2，然后看余数”的方式相比，小数部分转换成二进制是用一个相似的反方向操作，就是乘以2，然后看看是否超过1。如果超过1，我们就记下1，并把结果减去1，进一步循环操作。在这里，我们就会看到，0.1其实变成了一个无限循环的二进制小数，0.000110011。这里的“0011”会无限循环下去。

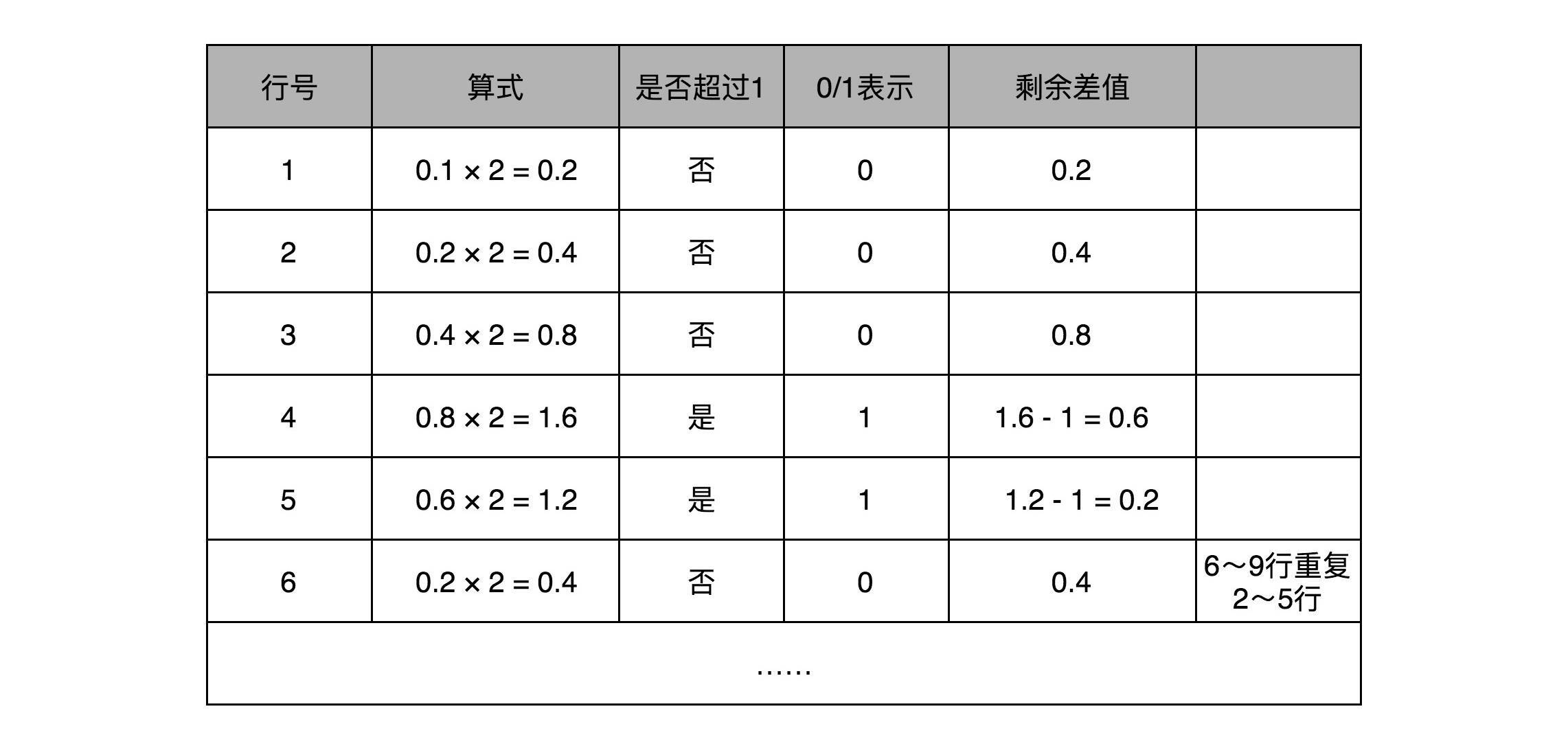
然后，我们把整数部分和小数部分拼接在一起，9.1这个十进制数就变成了1001.000110011…这样一个二进制表示。

上一讲我们讲过，浮点数其实是用二进制的科学计数法来表示的，所以我们可以把小数点左移三位，这个数就变成了：

$1.0010$$0011$$0011… × 2^3$

那这个二进制的科学计数法表示，我们就可以对应到了浮点数的格式里了。这里的符号位s = 0，对应的有效位f=001000110011…。因为f最长只有23位，那这里“0011”无限循环，最多到23位就截止了。于是，f=00100011001100110011 001。最后的一个“0011”循环中的最后一个“1”会被截断掉。对应的指数为e，代表的应该是3。因为指数位有正又有负，所以指数位在127之前代表负数，之后代表正数，那3其实对应的是加上127的偏移量130，转化成二进制，就是130，对应的就是指数位的二进制，表示出来就是10000010。

然后，我们把“s+e+f”拼在一起，就可以得到浮点数9.1的二进制表示了。最终得到的二进制表示就变成了：

010000010 0010 0011001100110011 001

如果我们再把这个浮点数表示换算成十进制，实际准确的值是9.09999942779541015625。相信你现在应该不会感觉奇怪了。

我在这里放一个链接，这里提供了直接交互式地设置符号位、指数位和有效位数的操作。你可以直观地看到，32位浮点数每一个bit的变化，对应的有效位数、指数会变成什么样子以及最后的十进制的计算结果是怎样的。

这个也解释了为什么，在上一讲一开始，0.3+0.6=0.899999。因为0.3转化成浮点数之后，和这里的9.1一样，并不是精确的0.3了，0.6和0.9也是一样的，最后的计算会出现精度问题。

浮点数的加法和精度损失

搞清楚了怎么把一个十进制的数值，转化成IEEE-754标准下的浮点数表示，我们现在来看一看浮点数的加法是怎么进行的。其实原理也很简单，你记住六个字就行了，那就是先对齐、再计算。

两个浮点数的指数位可能是不一样的，所以我们要把两个的指数位，变成一样的，然后只去计算有效位的加法就好了。

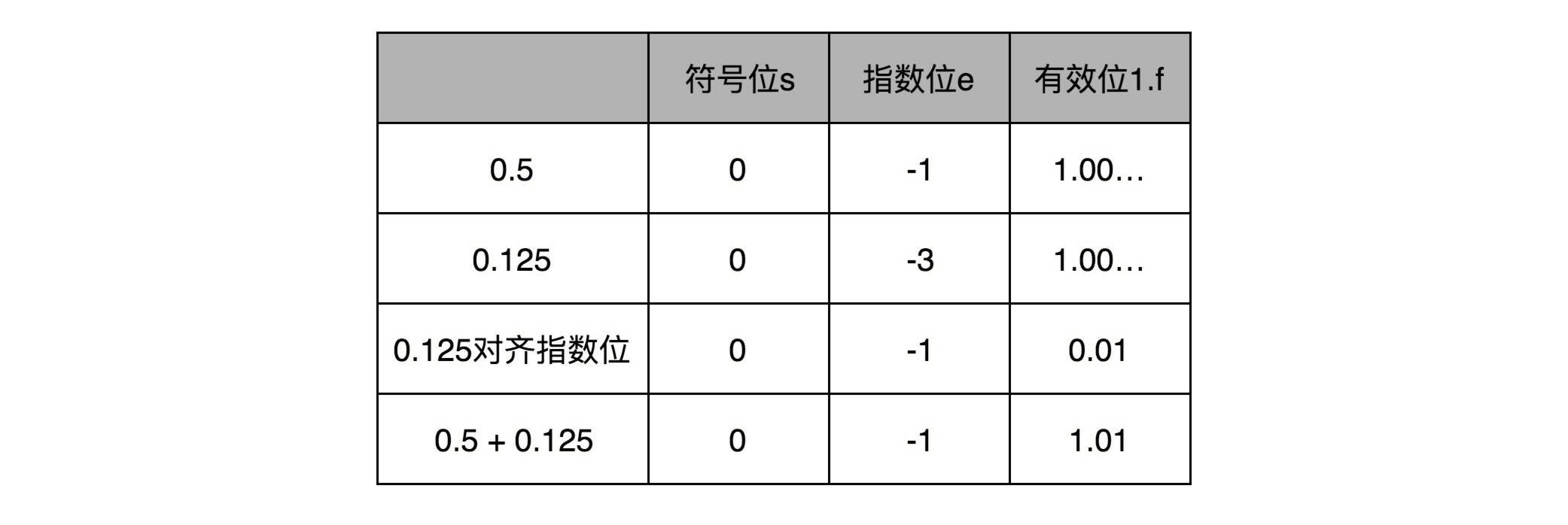
比如0.5，表示成浮点数，对应的指数位是-1，有效位是00…（后面全是0，记住f前默认有一个1）。0.125表示成浮点数，对应的指数位是-3，有效位也还是00…（后面全是0，记住f前默认有一个1）。

那我们在计算0.5+0.125的浮点数运算的时候，首先要把两个的指数位对齐，也就是把指数位都统一成两个其中较大的-1。对应的有效位1.00…也要对应右移两位，因为f前面有一个默认的1，所以就会变成0.01。然后我们计算两者相加的有效位1.f，就变成了有效位1.01，而指数位是-1，这样就得到了我们想要的加法后的结果。

实现这样一个加法，也只需要位移。和整数加法类似的半加器和全加器的方法就能够实现，在电路层面，也并没有引入太多新的复杂性。

同样的，你可以用刚才那个链接来试试看，我们这个加法计算的浮点数的结果是不是正确。

回到浮点数的加法过程，你会发现，其中指数位较小的数，需要在有效位进行右移，在右移的过程中，最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数，在加法发生之前，就丢失精度。两个相加数的指数位差的越大，位移的位数越大，可能丢失的精度也就越大。当然，也有可能你的运气非常好，右移丢失的有效位都是0。这种情况下，对应的加法虽然丢失了需要加的数字的精度，但是因为对应的值都是0，实际的加法的数值结果不会有精度损失。

32位浮点数的有效位长度一共只有23位，如果两个数的指数位差出23位，较小的数右移24位之后，所有的有效位就都丢失了。这也就意味着，虽然浮点数可以表示上到$3.40×10^{{38}$，下到$1.17×10}$，也就是差不多1600万倍，那这两个数相加之后，结果完全不会变化。}$这样的数值范围。但是在实际计算的时候，只要两个数，差出$2^{24

你可以试一下，我下面用一个简单的Java程序，让一个值为2000万的32位浮点数和1相加，你会发现，+1这个过程因为精度损失，被“完全抛弃”了。

public class FloatPrecision {
  public static void main(String[] args) {
    float a = 20000000.0f;
    float b = 1.0f;
    float c = a + b;
    System.out.println("c is " + c);
    float d = c - a;
    System.out.println("d is " + d);
  }
}

对应的输出结果就是：

c is 2.0E7
d is 0.0

Kahan Summation算法

那么，我们有没有什么办法来解决这个精度丢失问题呢？虽然我们在计算浮点数的时候，常常可以容忍一定的精度损失，但是像上面那样，如果我们连续加2000万个1，2000万的数值都会被精度损失丢掉了，就会影响我们的计算结果。

一个常见的应用场景是，在一些“积少成多”的计算过程中，比如在机器学习中，我们经常要计算海量样本计算出来的梯度或者loss，于是会出现几亿个浮点数的相加。每个浮点数可能都差不多大，但是随着累积值的越来越大，就会出现“大数吃小数”的情况。

我们可以做一个简单的实验，用一个循环相加2000万个1.0f，最终的结果会是1600万左右，而不是2000万。这是因为，加到1600万之后的加法因为精度丢失都没有了。这个代码比起上面的使用2000万来加1.0更具有现实意义。

public class FloatPrecision {
  public static void main(String[] args) {
    float sum = 0.0f;
    for (int i = 0; i < 20000000; i++) {
        float x = 1.0f;
        sum += x;       
    }
    System.out.println("sum is " + sum);   
  } 
}

对应的输出结果是：

sum is 1.6777216E7

面对这个问题，聪明的计算机科学家们也想出了具体的解决办法。他们发明了一种叫作Kahan Summation的算法来解决这个问题。算法的对应代码我也放在文稿中了。从中你可以看到，同样是2000万个1.0f相加，用这种算法我们得到了准确的2000万的结果。

public class KahanSummation {
  public static void main(String[] args) {
    float sum = 0.0f;
    float c = 0.0f;
    for (int i = 0; i < 20000000; i++) {
        float x = 1.0f;
        float y = x - c;
        float t = sum + y;
        c = (t-sum)-y;
        sum = t;        
    }
    System.out.println("sum is " + sum);   
  } 
}

对应的输出结果就是：

sum is 2.0E7

其实这个算法的原理其实并不复杂，就是在每次的计算过程中，都用一次减法，把当前加法计算中损失的精度记录下来，然后在后面的循环中，把这个精度损失放在要加的小数上，再做一次运算。

如果你对这个背后的数学原理特别感兴趣，可以去看一看Wikipedia链接里面对应的数学证明，也可以生成一些数据试一试这个算法。这个方法在实际的数值计算中也是常用的，也是大量数据累加中，解决浮点数精度带来的“大数吃小数”问题的必备方案。

总结延伸

到这里，我们已经讲完了浮点数的表示、加法计算以及可能会遇到的精度损失问题。可以看到，虽然浮点数能够表示的数据范围变大了很多，但是在实际应用的时候，由于存在精度损失，会导致加法的结果和我们的预期不同，乃至于完全没有加上的情况。

所以，一般情况下，在实践应用中，对于需要精确数值的，比如银行存款、电商交易，我们都会使用定点数或者整数类型。

比方说，你一定在MySQL里用过decimal(12,2)，来表示订单金额。如果我们的银行存款用32位浮点数表示，就会出现，马云的账户里有2千万，我的账户里只剩1块钱。结果银行一汇总总金额，那1块钱在账上就“不翼而飞”了。

而浮点数呢，则更适合我们不需要有一个非常精确的计算结果的情况。因为在真实的物理世界里，很多数值本来就不是精确的，我们只需要有限范围内的精度就好了。比如，从我家到办公室的距离，就不存在一个100%精确的值。我们可以精确到公里、米，甚至厘米，但是既没有必要、也没有可能去精确到微米乃至纳米。

对于浮点数加法中可能存在的精度损失，特别是大量加法运算中累积产生的巨大精度损失，我们可以用Kahan Summation这样的软件层面的算法来解决。

好了，到了这里，我已经把浮点数讲透了。希望你能从数据的表示、加法的实现，乃至实践应用、数值算法层面能够体会到，搞清楚一个计算机问题的基本原理，其实能够帮助你理解它的实践应用，乃至找到在特定问题下的可行解决方案。接下来，我们要深入到CPU的构造，去理解计算机组成原理。

课后思考

这两节我讲的都是32位浮点数，那么对于64位浮点数的加法，两个数相差多少的情况后，较小的哪个数在加法过程中会完全丢失呢？

欢迎你在留言区写下你的思考和疑问，和大家一起探讨。你也可以把今天的文章分享给你朋友，和他一起学习和进步。

精选留言（15）

奕 👍（16） 💬（5）
老师，这里我用 JS 代码实验了一下，JS 中的数值类型都是 IEEE754实现的浮点数类型： let a = 20000000; let b = 1; let c = a + b; console.log("c is " + c); let d = c - a; console.log("d is " + d); 输出是： // "c is 20000001" // "d is 1" 然后2千万个数相加： let result = 0; for (let j = 0; j < 20000000; j++) { result ++; }; console.log('result', result) // result 20000000 这里都是正确的，是自己实现了 Kahan Summation 算法吗？还是其他的原因？
2019-06-06

有米 👍（33） 💬（10）
decimal是如何实现保证不丢精度呢？
2019-05-31

Wayne 👍（25） 💬（1）
总感觉文中Kahan Summation代码的物理意义有点难以理解，写了个一个相对好一点理解的版本，仅供参考哈~ public static void main(String[] args) { float res = 0.0f; float remain = 0.0f; for (int i = 0; i < 20000000; i++) { float cur = 1.0f; float needToAdd = cur + remain; float nextRes = res + needToAdd; remain = needToAdd - (nextRes - res); res = nextRes; } System.out.println(res); }
2020-05-13

haoly1989 👍（25） 💬（0）
课后思考题解答：首先，64位浮点数的表示方法如下：符号位是1位，指数部分为11位，尾数部分为52位；其次，应用本节的可知，当做加法的两个64位的浮点数的指数位相差52位后，较小的那个数就会因为要右移53位导致有效位数完全丢失；最后，精度缺失问题同样可以使用`Kahan Summation`算法来补偿；
2019-08-15

Junho 👍（12） 💬（4）
老师好。平时会听说一种说法：在现代CPU下，定点数的执行效率比浮点数慢一到两个数量级。不知这个说法是否合理？如果合理的话，原理是什么呢？对于这两种表示法，在工作中的应用：游戏中涉及要求计算一致性的场合，如王者荣耀的网络同步方案。王者的同步方案是帧同步，在这个方案下，需要确保逻辑层的所有计算，在所有硬件下都是完全一致的，否则同步就会出现灾难性的后果。据找得到的资料，王者官方的分享是说，他们是用分数来代替浮点数的（分子和分母分别用整数表示），但没提及不用定点数的缘由。倒是腾讯另外某位技术专家，就提及了浮点数与定点数在执行效率上的差异，但没涉及原理说明，所以想请教一下老师这个问题。谢谢！
2019-06-20

有铭 👍（9） 💬（0）
decimal难道就是所谓定点数？Java里的BigDecimal的原理是什么？
2019-05-31

初心丶可曾記 👍（8） 💬（0）
64位浮点数，有效位是52位,所以相差2^53会丢失较小的数
2019-05-31

逍遥思 👍（4） 💬（1）
对Kahan Summation算法的理解： x，本轮要加的数第一个c，截止上一轮损失的精度第二个c，截止本轮损失的精度 y，本轮要加的数与之前累计损失的精度之和前两个sum，上一轮的求和结果 t和第三个sum，本轮的求和结果
2019-06-16

humor 👍（4） 💬（0）
对于64位的符点数，符号位是52位，所以应该是如果两个相差2^53倍及以上的数相加，较小的数会完全丢失吧。
2019-05-31

小广 👍（3） 💬（1）
吴老师好，既然9.1按浮点数合适存储起来的时候，精度已经损失了，那为什么在程序里面定义了一个变量的值为9.1后再打印结果，它还是显示9.1，而不是那个在浮点数格式中存储的不精确的的小数位很长的数呢？
2019-10-31

-W.LI- 👍（3） 💬（1）
老师好!我能说我没看懂么。。。f怎么算知道了e那个3怎么来的。9.1那个。。
2019-06-16

小木匠 👍（3） 💬（0）
老师，在Kahan 算法里，如果累积的损失精度c也不能达到1600万的条件，是不是也就不能被累加呢？比如做1亿6千万零9次加1计算，这9次是不是也就加不上了呢
2019-06-14

Null 👍（2） 💬（0）
其实kahan summation其实就是如果本次加会发生大数吃小数，那么留着跟下次的一起加，直到不会被吃掉，就加上了。积少成多，1你把我吃了，等我累加到一定数，两者的“指数差”没有那么大了，看你还敢吃我不。
2022-03-31

dog_brother 👍（2） 💬（0）
另外还有一个技巧，如果数量较多的浮点数相加，可以先加小数，再加大数，减少误差。
2021-05-13

supermouse 👍（2） 💬（2）
老师，我想问一个问题，为什么19000000.0f+1.0f=19000000.0f，而19000002.0f+1.0f=19000004.0f？（数字后面跟个f代表这个数是float类型） 19000000.0f+1.0f=19000000.0f 我能理解，因为大数吃小数，在对阶的时候 1.0f 的有效数位右移了 24 位导致精度损失，但是 19000002.0f+1.0f=19000004.0f 的结果为什么不是 19000002.0f 而是 19000004.0f呢？
2019-11-05