24丨索引的原理：我们为什么用B+树来做索引？

上节课我讲到了索引的作用，是否需要建立索引，以及建立什么样的索引，需要我们根据实际情况进行选择。我之前说过，索引其实就是一种数据结构，那么今天我们就来看下，索引的数据结构究竟是怎样的？对索引底层的数据结构有了更深入的了解后，就会更了解索引的使用原则。

今天的文章内容主要包括下面几个部分：

为什么索引要存放到硬盘上？如何评价索引的数据结构设计的好坏？
使用平衡二叉树作为索引的数据结构有哪些不足？
B树和B+树的结构是怎样的？为什么我们常用B+树作为索引的数据结构？

如何评价索引的数据结构设计好坏

数据库服务器有两种存储介质，分别为硬盘和内存。内存属于临时存储，容量有限，而且当发生意外时（比如断电或者发生故障重启）会造成数据丢失；硬盘相当于永久存储介质，这也是为什么我们需要把数据保存到硬盘上。

虽然内存的读取速度很快，但我们还是需要将索引存放到硬盘上，这样的话，当我们在硬盘上进行查询时，也就产生了硬盘的I/O操作。相比于内存的存取来说，硬盘的I/O存取消耗的时间要高很多。我们通过索引来查找某行数据的时候，需要计算产生的磁盘I/O次数，当磁盘I/O次数越多，所消耗的时间也就越大。如果我们能让索引的数据结构尽量减少硬盘的I/O操作，所消耗的时间也就越小。

二叉树的局限性

二分查找法是一种高效的数据检索方式，时间复杂度为O(log2n)，是不是采用二叉树就适合作为索引的数据结构呢？

我们先来看下最基础的二叉搜索树（Binary Search Tree），搜索某个节点和插入节点的规则一样，我们假设搜索插入的数值为key：

如果key大于根节点，则在右子树中进行查找；
如果key小于根节点，则在左子树中进行查找；
如果key等于根节点，也就是找到了这个节点，返回根节点即可。

举个例子，我们对数列（34，22，89，5，23，77，91）创造出来的二分查找树如下图所示：

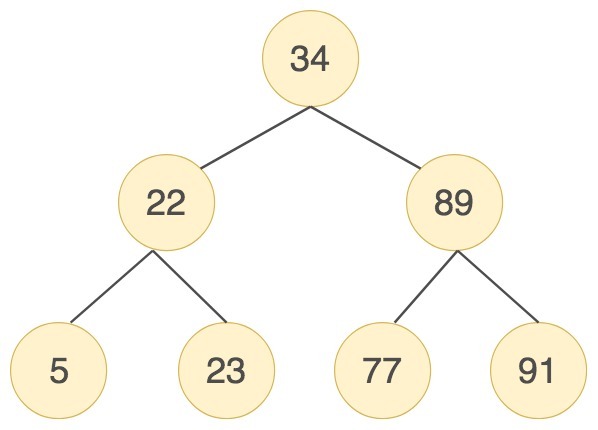
但是存在特殊的情况，就是有时候二叉树的深度非常大。比如我们给出的数据顺序是(5, 22, 23, 34, 77, 89, 91)，创造出来的二分搜索树如下图所示：

你能看出来第一个树的深度是3，也就是说最多只需3次比较，就可以找到节点，而第二个树的深度是7，最多需要7次比较才能找到节点。

第二棵树也属于二分查找树，但是性能上已经退化成了一条链表，查找数据的时间复杂度变成了O(n)。为了解决这个问题，人们提出了平衡二叉搜索树（AVL树），它在二分搜索树的基础上增加了约束，每个节点的左子树和右子树的高度差不能超过1，也就是说节点的左子树和右子树仍然为平衡二叉树。

这里说一下，常见的平衡二叉树有很多种，包括了平衡二叉搜索树、红黑树、数堆、伸展树。平衡二叉搜索树是最早提出来的自平衡二叉搜索树，当我们提到平衡二叉树时一般指的就是平衡二叉搜索树。事实上，第一棵树就属于平衡二叉搜索树，搜索时间复杂度就是O(log2n)。

我刚才提到过，数据查询的时间主要依赖于磁盘I/O的次数，如果我们采用二叉树的形式，即使通过平衡二叉搜索树进行了改进，树的深度也是O(log2n)，当n比较大时，深度也是比较高的，比如下图的情况：

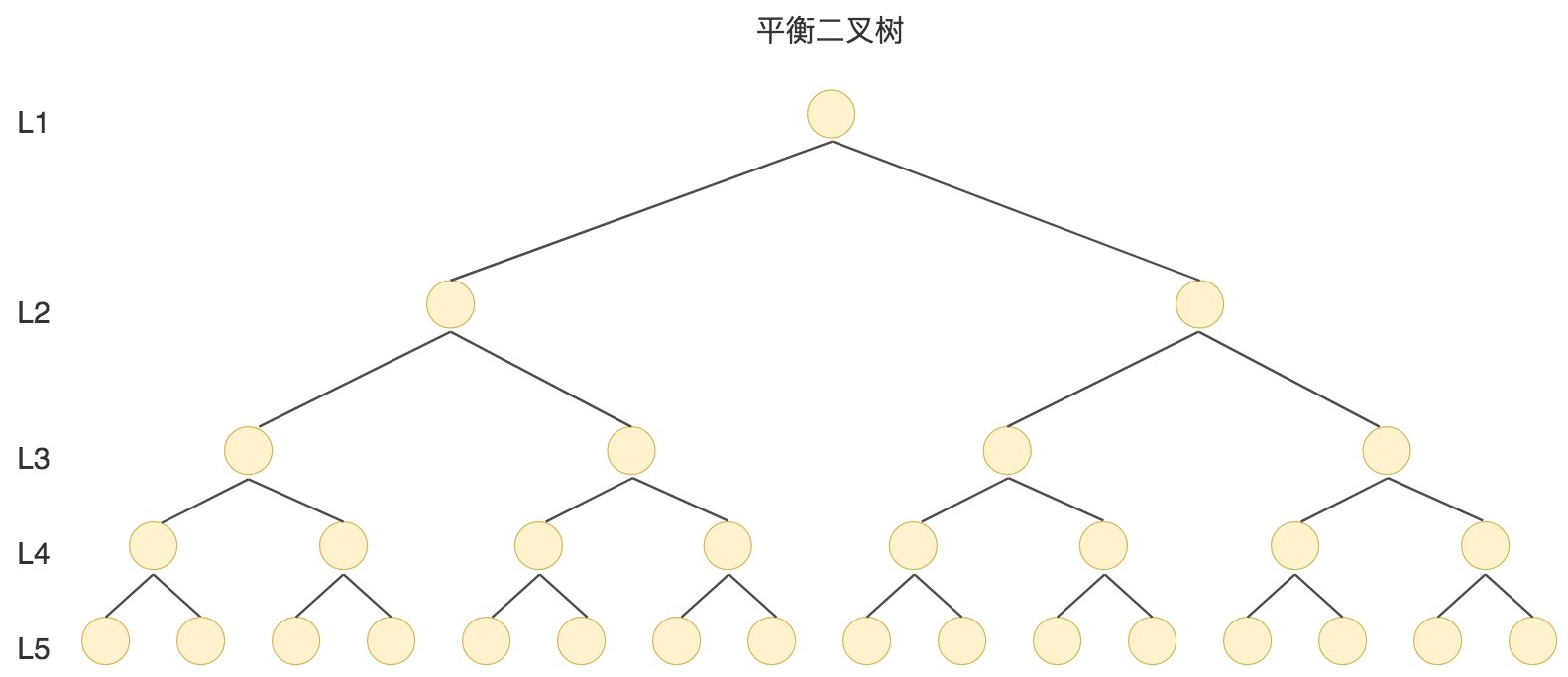
每访问一次节点就需要进行一次磁盘I/O操作，对于上面的树来说，我们需要进行5次I/O操作。虽然平衡二叉树比较的效率高，但是树的深度也同样高，这就意味着磁盘I/O操作次数多，会影响整体数据查询的效率。

针对同样的数据，如果我们把二叉树改成M叉树（M>2）呢？当M=3时，同样的31个节点可以由下面的三叉树来进行存储：

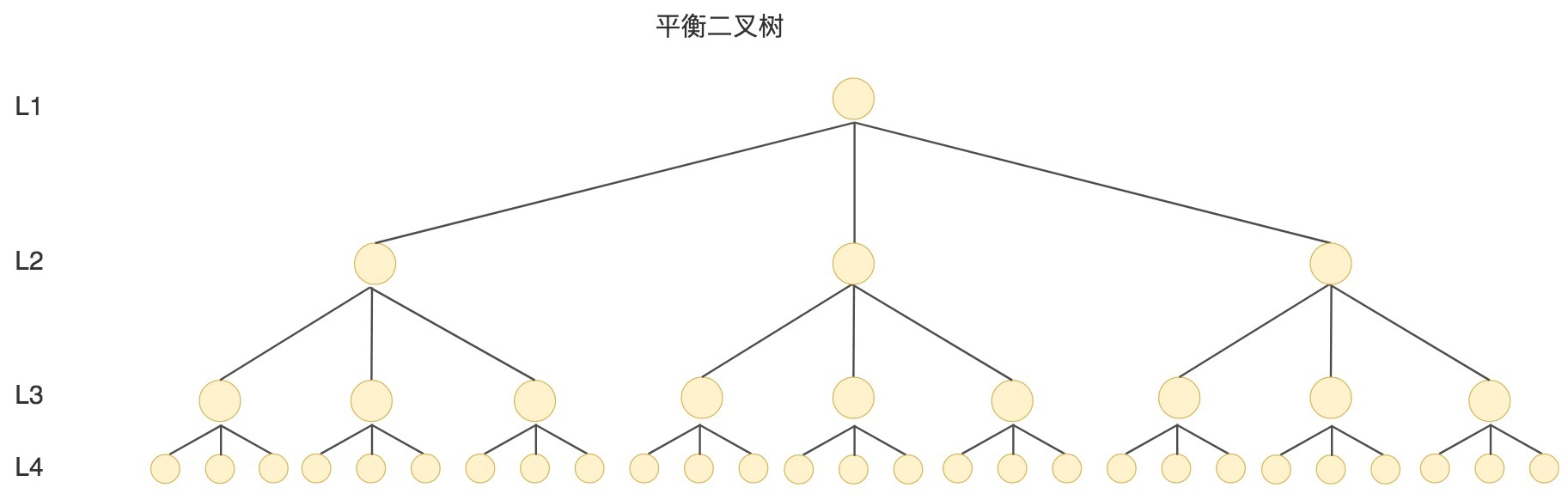
你能看到此时树的高度降低了，当数据量N大的时候，以及树的分叉数M大的时候，M叉树的高度会远小于二叉树的高度。

什么是B树

如果用二叉树作为索引的实现结构，会让树变得很高，增加硬盘的I/O次数，影响数据查询的时间。因此一个节点就不能只有2个子节点，而应该允许有M个子节点(M>2)。

B树的出现就是为了解决这个问题，B树的英文是Balance Tree，也就是平衡的多路搜索树，它的高度远小于平衡二叉树的高度。在文件系统和数据库系统中的索引结构经常采用B树来实现。

B树的结构如下图所示：

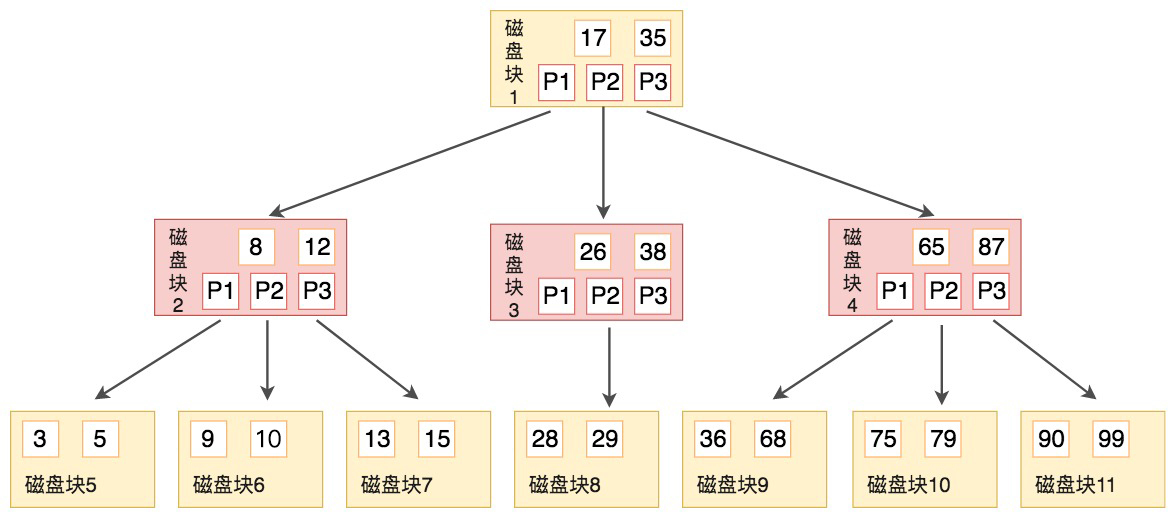
B树作为平衡的多路搜索树，它的每一个节点最多可以包括M个子节点，M称为B树的阶。同时你能看到，每个磁盘块中包括了关键字和子节点的指针。如果一个磁盘块中包括了x个关键字，那么指针数就是x+1。对于一个100阶的B树来说，如果有3层的话最多可以存储约100万的索引数据。对于大量的索引数据来说，采用B树的结构是非常适合的，因为树的高度要远小于二叉树的高度。

一个M阶的B树（M>2）有以下的特性：

根节点的儿子数的范围是[2,M]。
每个中间节点包含k-1个关键字和k个孩子，孩子的数量=关键字的数量+1，k的取值范围为[ceil(M/2), M]。
叶子节点包括k-1个关键字（叶子节点没有孩子），k的取值范围为[ceil(M/2), M]。
假设中间节点节点的关键字为：Key[1], Key[2], …, Key[k-1]，且关键字按照升序排序，即Key[i]<Key[i+1]。此时k-1个关键字相当于划分了k个范围，也就是对应着k个指针，即为：P[1], P[2], …, P[k]，其中P[1]指向关键字小于Key[1]的子树，P[i]指向关键字属于(Key[i-1], Key[i])的子树，P[k]指向关键字大于Key[k-1]的子树。
所有叶子节点位于同一层。

上面那张图所表示的B树就是一棵3阶的B树。我们可以看下磁盘块2，里面的关键字为（8，12），它有3个孩子(3，5)，(9，10) 和 (13，15)，你能看到(3，5)小于8，(9，10)在8和12之间，而(13，15)大于12，刚好符合刚才我们给出的特征。

然后我们来看下如何用B树进行查找。假设我们想要查找的关键字是9，那么步骤可以分为以下几步：

我们与根节点的关键字(17，35）进行比较，9小于17那么得到指针P1；
按照指针P1找到磁盘块2，关键字为（8，12），因为9在8和12之间，所以我们得到指针P2；
按照指针P2找到磁盘块6，关键字为（9，10），然后我们找到了关键字9。

你能看出来在B树的搜索过程中，我们比较的次数并不少，但如果把数据读取出来然后在内存中进行比较，这个时间就是可以忽略不计的。而读取磁盘块本身需要进行I/O操作，消耗的时间比在内存中进行比较所需要的时间要多，是数据查找用时的重要因素，B树相比于平衡二叉树来说磁盘I/O操作要少，在数据查询中比平衡二叉树效率要高。

什么是B+树

B+树基于B树做出了改进，主流的DBMS都支持B+树的索引方式，比如MySQL。B+树和B树的差异在于以下几点：

有 k 个孩子的节点就有k个关键字。也就是孩子数量=关键字数，而B树中，孩子数量=关键字数+1。
非叶子节点的关键字也会同时存在在子节点中，并且是在子节点中所有关键字的最大（或最小）。
非叶子节点仅用于索引，不保存数据记录，跟记录有关的信息都放在叶子节点中。而B树中，非叶子节点既保存索引，也保存数据记录。
所有关键字都在叶子节点出现，叶子节点构成一个有序链表，而且叶子节点本身按照关键字的大小从小到大顺序链接。

下图就是一棵B+树，阶数为3，根节点中的关键字1、18、35分别是子节点（1，8，14），（18，24，31）和（35，41，53）中的最小值。每一层父节点的关键字都会出现在下一层的子节点的关键字中，因此在叶子节点中包括了所有的关键字信息，并且每一个叶子节点都有一个指向下一个节点的指针，这样就形成了一个链表。

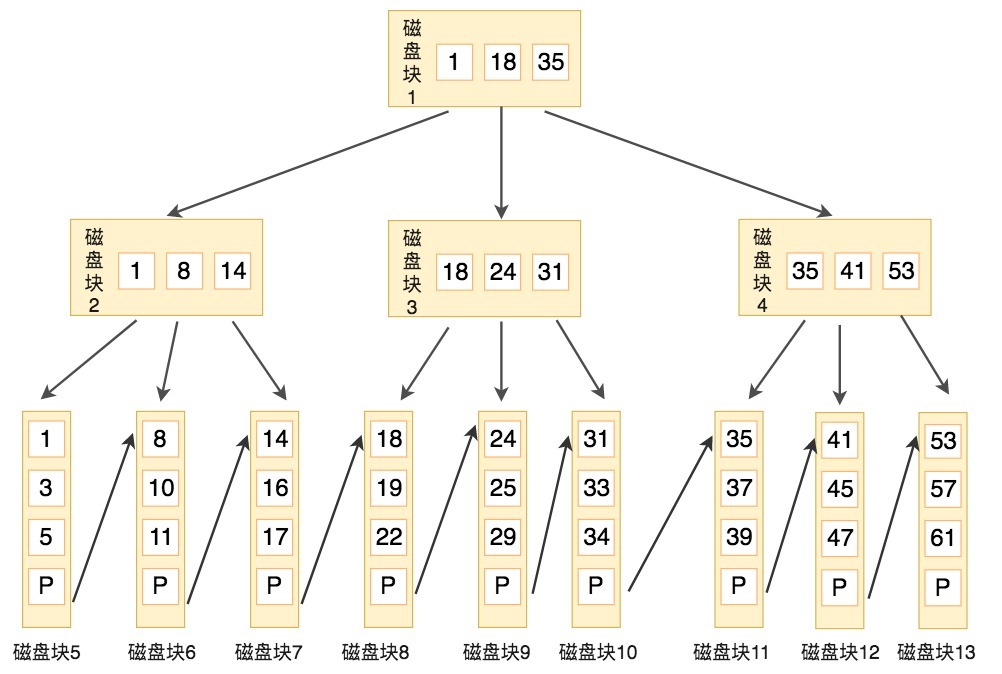
比如，我们想要查找关键字16，B+树会自顶向下逐层进行查找：

与根节点的关键字(1，18，35)进行比较，16在1和18之间，得到指针P1（指向磁盘块2）
找到磁盘块2，关键字为（1，8，14），因为16大于14，所以得到指针P3（指向磁盘块7）
找到磁盘块7，关键字为（14，16，17），然后我们找到了关键字16，所以可以找到关键字16所对应的数据。

整个过程一共进行了3次I/O操作，看起来B+树和B树的查询过程差不多，但是B+树和B树有个根本的差异在于，B+树的中间节点并不直接存储数据。这样的好处都有什么呢？

首先，B+树查询效率更稳定。因为B+树每次只有访问到叶子节点才能找到对应的数据，而在B树中，非叶子节点也会存储数据，这样就会造成查询效率不稳定的情况，有时候访问到了非叶子节点就可以找到关键字，而有时需要访问到叶子节点才能找到关键字。

其次，B+树的查询效率更高，这是因为通常B+树比B树更矮胖（阶数更大，深度更低），查询所需要的磁盘I/O也会更少。同样的磁盘页大小，B+树可以存储更多的节点关键字。

不仅是对单个关键字的查询上，在查询范围上，B+树的效率也比B树高。这是因为所有关键字都出现在B+树的叶子节点中，并通过有序链表进行了链接。而在B树中则需要通过中序遍历才能完成查询范围的查找，效率要低很多。

总结

磁盘的I/O操作次数对索引的使用效率至关重要。虽然传统的二叉树数据结构查找数据的效率高，但很容易增加磁盘I/O操作的次数，影响索引使用的效率。因此在构造索引的时候，我们更倾向于采用“矮胖”的数据结构。

B树和B+树都可以作为索引的数据结构，在MySQL中采用的是B+树，B+树在查询性能上更稳定，在磁盘页大小相同的情况下，树的构造更加矮胖，所需要进行的磁盘I/O次数更少，更适合进行关键字的范围查询。

今天我们对索引的底层数据结构进行了学习，你能说下为什么数据库索引采用B+树，而不是平衡二叉搜索树吗？另外，B+树和B树在构造和查询性能上有什么差异呢？

欢迎你在评论区写下你的思考，也欢迎把这篇文章分享给你的朋友或者同事，一起来交流。

精选留言（15）

Goal 👍（105） 💬（4）
一、数据库索引，为什么不适用用二叉树： 1. 平衡二叉树必须满足（所有节点的左右子树高度差不超过1）。执行插入还是删除操作，只要不满足上述条件，就要通过旋转来保持平衡，而旋转是非常耗时的，所以AVL树适合用于查找多的情况。 2. 二叉树的数据结构，会导致“深度”，比较深，这种“瘦高”的特性，加大了平均查询的磁盘IO次数，随着数据量的增多，查询效率也会受到影响；二、B+ 树和 B 树在构造和查询性能上有什么差异呢？ B+ 树的中间节点并不直接存储数据。 1. B+树的查询效率更加稳定：由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。 2. B+树的磁盘读写代价更低：B+树的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对B树更小，如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多，一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。 3、由于B+树的数据都存储在叶子结点中，分支结点均为索引，方便扫库，只需要扫一遍叶子结点即可，但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要进行一次中序遍历按序来扫，所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引。
2019-08-05

Monday 👍（14） 💬（3）
B树和B+树的区别： 1、B树非叶子结点存储数据；B+树非叶子结点不存储数据只存索引。 2、B树叶子结点没有使用双向链表串连；B+树叶子结点使用双向链表进行串连，为了支持区间查询。
2019-08-08

ack 👍（13） 💬（3）
1.为什么数据库索引采用 B+ 树，而不是平衡二叉搜索树？数据库索引存储在磁盘上，平衡二叉树虽然查找效率高，但“高瘦”，进行的IO次数比平衡二叉搜索树多。 2.B+ 树和 B 树在构造和查询性能上差异？（1）B树的每个节点含有卫星数据，而B+树中间节点含有指向卫星数据的指针，叶子节点才存有卫星数据。这样一来每次进行B+树查询都需要查询到叶子节点，性能更稳定，而且B+树节点只存储指向卫星数据的指针，这样一个磁盘页能存储更多节点。（2）B+树范围查询更有优势，因为叶子节点直接串联成一条链表（3）B+树单一结点比起B树存储更多元素，IO更少
2019-08-05

mickey 👍（10） 💬（8）
请问，文中的B树图，元素“68”是在“65”到“85”之间，为什么属于第一棵子树呢？
2019-08-05

吃饭饭 👍（8） 💬（5）
【对于一个 100 阶的 B 树来说，如果有 3 层的话最多可以存储约 100 万的索引数据】是怎么计算出 100 万的，按照前面的描述指数是关键字的个数+1 没弄明白，求解答？
2019-08-05

吴小智 👍（6） 💬（1）
B+ 树中间节点只保存索引，不保存数据，所以一个节点能放更多的索引，同样的索引树，相比于 B 树，B + 树的深度会更少。
2019-08-21

雪飞鸿 👍（4） 💬（2）
网上还看到B-tree是和B tree一个意思吗？
2019-09-18

夜路破晓 👍（4） 💬（1）
记得刚接触编程的时候，很不习惯计数要从0开始，后来用围栏法勉强不会搞错计数顺序了，还是一直不解为什么要这样设计。今天看老师讲解b树和b＋树，有个类似发现，b树就好像很多人习惯了的从1开始计数，或者举例说要把一段绳子截成三段，你只需截2次即可； b ＋树就好比用围栏隔出若干空间，比如隔出两块空间需要三个围栏板，脑海里联想下公测的蹲坑隔间就能理解了。按我的理解b＋树之所以显示优于b树，可能跟前后两端的数据空间有关，这跟将数据序列设计成从0开始计数而非从1开始是出于同样的考量。
2019-08-05

许童童 👍（4） 💬（1）
老师讲得好，深入浅出。
2019-08-05

程序员花卷 👍（3） 💬（1）
首先感谢前面认真学习数据结构的自己，这下不就用到了！所以学习这一节的时候就感觉非常爽！ 1、数据库索引为什么采用B+树而不采用平衡二叉搜索树？数据库的索引是存储在磁盘上的，每次查询都需要涉及I/O操作，I/O操作的次数越多，那么查询所化的时间就越长，性能也就越低，所以引入了平衡二叉搜索树来存储数据，本来平衡二叉搜索树的查询效率是非常高的，但是当数据量很大的时候，平衡二叉搜索树的高度就会很高，每次进行查询的时候也就需要经历很多的节点，自然也就增加了I/O操作的次数，严重的降低了性能，要是你查询的数据刚好在根节点那还好，都是一样的，但是这种情况的概率只有1%，属于极端情况(自己脑补)......所以在此引入了B+树这个数据结构（B树老师已经说得很清楚了，我就不说了），降低了树的高度，减少了I/O操作的次数，提高了查询的效率！ 2、B和B+树在构造上有什么差异吗？ B+树的查询效率更稳定的，因为每次都必须查询到叶子节点才能找到最终的数据，而B树查询的数据也许在叶节点上，也许在叶子节点上，这样就会造成查询的效率不稳定！ B+树的查询效率更高，因为B+树更矮更胖（肉多，哈哈），所以B+树的高度越小，查询时产生的I/O次数也就更少，性能自然就高！
2019-12-22

爱思考的仙人球 👍（3） 💬（2）
B+树查询效率更稳定，磁盘I/O次数更少
2019-10-20

未来的胡先森 👍（3） 💬（1）
为什么选用「 B+ 树」而不是「平衡二叉树」呢？老师在文章中已经给出了答案，「平衡二叉树」只有两个分支，而「 B+ 树」的分支大于等于 2，根据等比数列的公式可以得出，「 B+ 树」的层数只会小于「平衡二叉树」，层数越少，在查询时所需要的 I/O 操作（硬盘访问）就少，相对来说查询速度就快了，同时也提高了系统资源的利用率。「 B+ 树」和「 B 树」在构造和查询性能上的差别？老师在文章中也提到了，构造方面：最明显的莫过于「 B+ 树」非叶子结点并不存储数据，且所有数据节点串联（就是链表了），「 B 树」子结点带数据，且「兄弟结点」之间无串联。查询性能差异：我觉得很直观的体现在范围查询时，「 B+ 树」我们只需要知道范围的边界节点，然后遍历即可，而「 B 树」可能就需要一个个查找了。假设查询 [0,n-1] n 个数，「 B+ 树」的时间复杂度可以粗略看做 2logn+n (2logn : 两个范围边界值的查找)，而「 B 树」可能就是 nlogn ，范围越大，查询性能差异越明显。
2019-08-14

JustDoDT 👍（3） 💬（2）
这节厉害了，得多看几遍，慢慢消化。
2019-08-05

梁 👍（2） 💬（1）
为什么使用B+而不是B？稳定压倒一切！
2019-11-19

雪飞鸿 👍（2） 💬（1）
文中所说的关键字怎么理解？
2019-10-11