《一个数学家的叹息》 苗炜工作室解读

《一个数学家的叹息》| 苗炜工作室解读

关于作者

作者保罗·洛克哈特，是一位数学家。大概14岁时，他对数学产生浓厚兴趣，1990年在哥伦比亚大学获得博士学位后，洛克哈特先后在加州大学伯克利分校的数学科学研究中心（MSRI）和布朗大学任职。2000年加入纽约的独立学校圣安学校，教导从幼儿园到12年级的数学课至今。

关于本书

当代美国教育不能帮助孩子学好数学。数学应该像绘画、音乐和诗歌一样，数学是一门艺术，需要激发灵感；数学又和游戏一样，基于好奇心。他呼吁教育者反思和尝试改变自己的教学方式，带领孩子能够真正走进数学的世界，领略数学之美。

核心内容

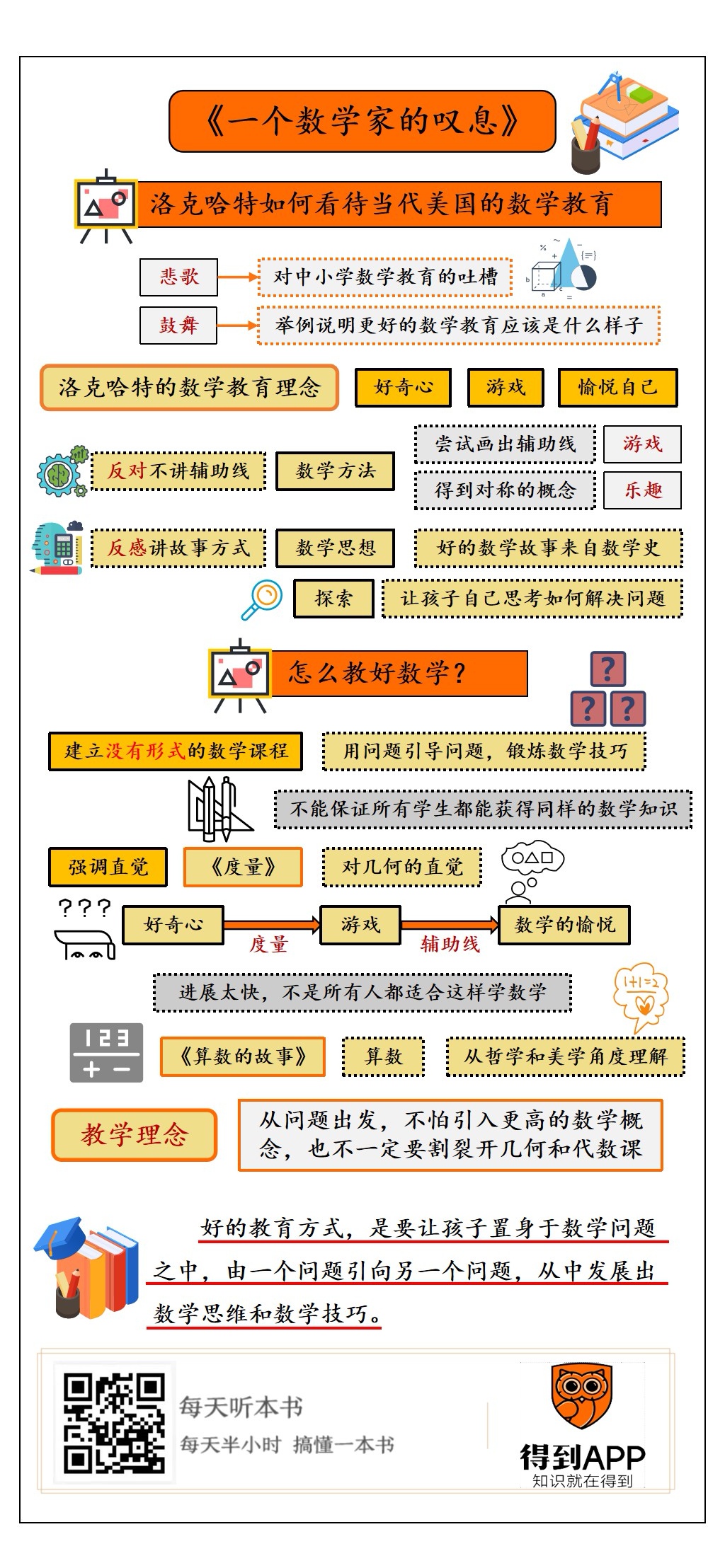
1.洛克哈特如何看待当代美国的数学教育？

2.结合他的另外两本书《算术的故事》和《度量》，来讲讲怎么教好数学。

你好，欢迎你每天听本书。今天我要解读的是《一个数学家的叹息》。这本书的作者保罗·洛克哈特，是一位数学家。他写这本书，是为了吐槽自己对美国中小学数学教育的不满。除了叹息和吐槽，他也会告诉我们，怎么更好地帮助孩子学习数学。

请你回想一下，我们上中学上小学的时候，数学经常是所有课程中最有地位的一门课，课程最多，作业也最多。为什么会这样呢？因为数学成绩，标志着智力水平。所以，老师和家长都很重视数学。光在学校里学，还不够，家长还会给孩子买各种参考书，报各种课外班。可效果呢？往往要看孩子的天分了。

怎么才能让孩子学好数学呢？

美国作家马克·吐温说过一句名言：我从来不让学校干扰我的教育。这本书作者洛克哈特肯定会表示赞同。他觉得，如今美国中小学的数学课程，不仅不能帮孩子学好数学，反而会干扰孩子，让他们学不好数学。

洛克哈特自己14岁的时候就对数学产生兴趣，但是，启发他的不是学校的数学课，而是课外阅读。在大学里上了一个学期的课之后，洛克哈特就退学，靠编程、当小学教师为生。后来，他跟加州大学的一位数学家合作，发表了多篇论文，才继续读他的研究生。后来，他在哥伦比亚大学获得博士学位，又在加州大学伯克利分校和布朗大学任教。

但是，洛克哈特对美国学校的数学教育一直有所不满。2002年，他写了一篇长文，叫《一个数学家的叹息》。他可不是长叹一声就完了。写完这篇文章，他就从大学里辞职，跑到纽约的一所K12学校，去教数学了。那意思是，我说你们不行，我来证明我行。

2007年，斯坦福大学的教授、数学家齐斯•德福林在美国数学协会的网站上发表了这篇文章，引起了广泛关注，这本书才能出版。德福林教授说：洛克哈特的观点并不新鲜，很多数学教授都表达过对中小学数学教育的不满。但是，洛克哈特这本书流露出对数学的巨大热情，并且真正对数学教育提出了自己的看法。每一个从事数学教育的人，每一个学龄孩子的家长，都应该看看这本书，因为它是对中小学数学教育做出的最好的评论。德福林教授还说，洛克哈特所主张的教学方法，不是每一个老师都能掌握的，但是，如果洛克哈特能来当我的数学老师，那我会非常高兴的。

我对这本书的解读，会分成两个部分。第一部分，我们来讲讲洛克哈特如何看待当代美国的数学教育。第二部分，我们结合他的另外两本书《算术的故事》和《度量》，来讲讲怎么教好数学。请注意，解读中会拿几个简单的数学题来举例说明，毕竟，我们解读的是一本数学书。

这本《一个数学家的叹息》，其实只是一篇很长的文章，翻译成中文不过三四万字。全书分为上下两篇，上篇的题目叫“悲歌”，是对中小学数学教育的吐槽；下篇的题目叫“鼓舞”，举例来说明更好的数学教育应该是什么样子。

洛克哈特以一个音乐家的噩梦开头。音乐家梦到，音乐教育就是要让孩子掌握音乐这种语言，先学音乐理论，学五线谱，理解什么叫五度循环，什么叫和声，什么叫复调，不许唱歌不许演奏乐器。因为演奏或者是聆听音乐是太高深的课题，上了大学才能学。洛克哈特说，音乐当然不能这样教，但是，今天美国的数学恰恰是这样教的。

这是洛克哈特的不满。在他看来，学数学，应该像学艺术一样。他引用英国数学家哈代的话：一个数学家，就像一位画家或诗人，是模式的创造者。

把数学比作艺术，说数学的美学原则就是简单，这种说法并不新鲜。洛克哈特的数学教育理念有什么特别之处呢？

得到“每天听本书”栏目里，解读过一本书叫《为什么学生不喜欢上学》。那本书开篇就说，我们的大脑不是用来思考的，大脑真正的作用是让你避免思考，因为它并不擅长。这本书其实也是一本给老师看的参考书。它告诉我们，孩子不喜欢思考，所以要降低难度，让他们尝到思考的乐趣，才会喜欢学习。洛克哈特显然不会同意这种教育理念。他说，面对数学问题，要有游戏精神。想要学好数学，学生要有好奇心，他必须想要知道答案，而且要不断尝试，乐在其中，用自己的想象力，来娱乐自己。

好奇心，把做题当游戏，还要从自己的想象力中得到乐趣。这对学生的要求是不是太高了？数学能当游戏来玩吗？

我们来看一道中学数学题。请你想象一个长方形中，有一个三角形，三角形的底边就是长方形的底边，三角形的顶点位于长方形上面那条边的任意一点，那么这个三角形的面积，是长方形面积的三分之二还是二分之一？

解法很简单。洛克哈特做了一条辅助线，从三角形顶点，画一条垂直于底边的线。这条线把长方形分成了两个部分。这两个部分，都被三角形的斜边切成了一半。显然，这个三角形的面积，正好是长方形面积的一半。

这道题，我们在数学课上不是这么学的。数学老师只是告诉你一个公式，三角形面积等于二分之一的底乘高（A=1/2bh），然后就让你在习题中反复应用。

洛克哈特说，他不是反对公式，而是反对不讲辅助线。三角形面积是长方形面积一半，这个事实不重要，重要的是用辅助线来切割。这个巧妙构想会让孩子明白什么叫数学方法，可以激发他更多的构想。如果他不懂得欣赏这条辅助线，就不能理解数学的美感和想象力。洛克哈特的意思是，尝试画出这条辅助线就是把做题当游戏，由此得到对称的概念，就是乐趣。

洛克哈特不仅反对直接告诉孩子结果，他也非常反感用讲故事的方式来讲数学。比如，玛丽亚的年龄是她七年前年龄的两倍，请问玛丽亚几岁了。他说，你都知道她的年龄是她七年前的两倍这样重要的信息了，你怎么可能不知道玛丽亚现在几岁呢？这道题的关键，其实就是两个数字之和与两个数字之差的关系。这样看起来，数学显得不太友善，但是，想让数学看起来跟生活有关，把数学弄得友善，这只是教师的做作。

洛克哈特非常骄傲地说，不要把数学变得有趣。你不懂，才会觉得它无趣，你懂了，它就乐趣无穷。数学的美就在于它跟日常生活没关系，所以它才有趣。我们学校里为了让孩子学会计算圆周的长度和圆的面积，会编一套圆周先生和面积太太的对话，这是最无聊的故事。好的数学故事来自数学史，要讲清楚圆，就要讲数学史上人类为了测量曲线所做的种种努力。

洛克哈特的观点，很有挑战性，也很有颠覆性。我们经常会觉得孩子不懂，不想他们解释太多，想解释也解释不清楚。比如说，小孩子知道三角形有三条边，四边形有四条边，知道五边形、六边形，乃至正十二边形、正十七边形。他可能会问你，圆有几条边？这是一个很难的问题。一般来说，我们为了图省事，都会说，圆有一条边，但这条边是曲线。我们很难跟小孩子解释，如果你把边理解为一条线段，那么圆有无数条边，多边形的边数越多，其形状、周长、面积就越接近于圆。所以，我们可以把圆看成是由无数个线段组成的正多边形。圆是一种概念性的图形。你如果这样跟孩子解释，孩子的脑子就乱掉了。

但洛克哈特就是要高估孩子的理解力。他觉得，要想让孩子理解圆的面积和周长，就要讲数学史上的欧多克索斯和阿基米德。欧多克索斯是公元前400年的古希腊数学家，他对数学的一个重要贡献是建立了严谨的穷竭法，并用它证明了一些重要的定理。中国古代也有割圆为方的数学思想，就是用圆内接正多边形的面积去无限逼近圆面积。但穷竭法、割圆为方，涉及极限和无限小的概念，如果沿着这个思路讲下去，就会讲到微积分。

你肯定会想，孩子能懂吗？洛克哈特回答：我并不抱这样的期望。我想说的是，现在的数学课程里，完全没有数学的艺术与发现，没有数学的历史和哲学，这是不对的。数学课，一方面孩子要懂得数学符号和数学基础知识，另一方面也要掌握数学思想。他还说，对于文学，我们就不会有这种怀疑。学习诗歌，并不是记得一大堆诗作，而是自己创作。

小孩子当然不可能在数学上有什么创作。洛克哈特想强调的是，数学是一种探索过程，任何一种心智上的敏锐，都来自自己解决问题。在数学教育中适当引入数学史内容，是让孩子思考去如何解决问题，而不是被告知该怎么解决问题。定义和公式并不能让学生更聪明。

我们来看洛克哈特在书里讲的一个例子。这个例子稍微需要一点计算，我们说慢一点。

数字有一个很神奇的现象，简单来说，就是把连续的奇数相加，会得到一个平方数。你想想，1加3等于4，4是2的平方；1加3加5等于9，9是3的平方；再继续算下去，1加3加5加7是16，16是4的平方；加到19，奇数之和是100，是10的平方。

这是个规律吗？奇数之和是一个平方数？洛克哈特说，目前我们还无法断言，就算检查100万个例子，也不能证明什么。实际上，在数学领域，关于整数就有数百个简单的问题，至今无解。但是，思考这个问题，是有意义的，把奇数相加跟算平方数，表面看起来是两个没关系的问题，为什么它们之间会有这种神秘的关联呢？他说，搞明白这个事情，才是你心智的进步，数学会让你的心智每天都受到这样的冲击。

在书里，洛克哈特是用图形来解释的。我把图片放到文稿中了，如果感兴趣，你也可以边看图，边听他的解答。

请你想象一个边长是3的正方形，在这个正方形里划一个“井”字，你会得到9个小方块。下面我们要做的是，从右上角开始，按照奇数把这些碎片拿出来。首先，拿出右上角的1片；然后拿出离这1片最近的3片，这3片会构成一个L形；接下来，再拿出一个更大的L形，也就是剩下的5片。我们拿出的数量，是相邻的3个奇数1、3、5，它们的和，就是这个边长为3的正方形，也就是3的平方。刚好符合我们前面说的规律，对吧？如果我们在这个正方形之外，再加上一个7片的L形，刚好可以组成一个更大的边长是4的正方形。你看，通过简单的图示，我们就能理解奇数之和跟平方数之间神秘的关联。

我们刚才说的这个例子，可能是这本书里最震慑的一个例子。奇数相加等于一个完全平方数，为什么？这就是好奇心。把完全平方数转化为一个正方形，然后圈出其中代表数字的方块。这是在游戏。发现其中的规律，把奇数之和与完全平方数的关系找出来，这就是愉悦自己。

洛克哈特说，这些才是我数学成长经验最重要的部分。

接下来第二部分，回到我们更关心的问题，如果领悟才是最重要的，那么我们到底应该如何教数学呢？

洛克哈特认为，我们应该建立一些没有形式的数学课程，学生遇到什么，就学什么。说得再具体以一点，就是用问题引导问题，由此锻炼数学的技巧。他说，这个想法可能有点儿疯狂，因为这样做，学校不能保证所有学生都能获得同样的数学知识。但是，学校本来就不该做这样的保证，因为人和人就是不一样的，一个高中毕业生不知道半角公式，也没什么。

话说至此，你应该可以看出，洛克哈特的教育理念有一定的危险。你要跟着他学数学，应付中考高考，怕是会出问题。但是，如果你对数学感兴趣，愿意在数学中获得更多的乐趣，那洛克哈特会是一个很好的老师。

书里有一个章节叫“中学几何：邪恶的工具”。这章里，他对美国的几何课狠狠地吐槽了一番。他说，中学的几何课，比披着羊皮的狼还糟糕。学校尝试用这个课程向学生介绍论证的方法，却摧毁了理性论证的本质，磨灭了学生对几何的喜欢，让他们永远不能以自然又直觉的方式来思考数学。

洛克哈特举了一个例子。两条交叉的直线，一个夹角等于与它相对的那个夹角。这个事，凭直觉就能看出来，但美国中学的几何课却需要你证明它，证明过程非常简单，但是看起来特别无趣。洛克哈特说，这本来应该是用最自然的语言写出的趣味论证，却被搞得沉闷、没有灵魂。直截了当的观察，写成了一堆假学问。学生要学数学论证，但是，只有当你发现事情违反直觉，或者有矛盾的时候，你才需要严格的证明。

教数学的时候，洛克哈特特别强调直觉。他那本讲几何的书《度量》，一开始就是在唤起我们对几何的直觉。这本书的第一页上画了一堆等边三角形、正方形和正六边形。如果你的孩子玩磁力贴，你就会发现，磁力贴最主要的形状就是这三种。或者，如果你装修过房子，你也会发现，瓷砖也大多都是正方形、正三角形和正六边形。洛克哈特说，我喜欢这几个形状，它们是对称的，每个边相等，每个角相等。

接着他把4个正方形摆成一个更大的正方形。4个正方形相交的那个点，正好有4个直角，一个直角的角度是90度，四个直角就是360度。在这里，洛克哈特引入了一个基本的概念，叫圆角，圆角就是360度的角。接着，他讲道：正三角形的内角是60度，6个正三角形围成一个360度的圆角，正6边形的内角是120度，3个正六边形正好围成一个360度的圆角。这几个形状为什么在磁力贴上很常见呢？因为它们更容易拼在一起，搭建成一个更大的形状。装修的时候用正方形或者长方形的瓷砖最多，也是这个道理，它们能更好地铺满地面。

我们知道，360度就是沿着一点转一圈，圆角就是360度。假设你沿着正三角形的三条边转上一圈，你就回到了原点，也就是完成了转360度。可是，三角形的内角之和是180度，这是怎么回事？这么说可能有点难理解，我们换一个更日常的例子。当你开车的时候，如果掉头，角度其实为零，但你要转180度。在这里，洛克哈特又引入内角外角的概念。我们直觉想到的0度，就是内角角度；掉头的时候实际转了180度。这就是外角的角度。当我们在三角形的三条边上行走时，转的并不是内角的角度，而是外角的角度。

《度量》这本书是一个很好的案例，生动地展示了洛克哈特的教学方法和教学理念。从好奇心出发，怎么度量，这是最基本的问题。然后，他开始带着我们在数学中游戏，在各种图形中画辅助线，把一个图形套入另一个图形，将代数公式用几何图形展示出来。问题一步步深入，我们因此得到了数学的愉悦。然而，整本书读下来，你会发现，开始几节的内容，也许适合放在初中一年级，后面的内容就到了高中二年级。如果用传统数学课程的眼光看，会觉得进展太快。难道这本书讲一年，就让一个刚明白360周角的人懂得微积分了吗？所以，不是所有人都适合这样学数学，但是，你不得不承认，洛克哈特开启了一段激动人心的数学之旅。

如果你已经忘记了中学数学的大部分内容，《度量》这本书会显得有点儿难。相比之下，《算术的故事》这本书看起来会轻松很多。这本书讲了怎么计数，古埃及人怎么算数，罗马人怎么算数，印度人怎么算，中国人和日本人怎么用算盘。这里，他就讲到了十进制和位值制的概念，讲了加减乘除。

《算术的故事》中这些数学史的内容并不新鲜，好多儿童数学启蒙绘本也会讲。洛克哈特并不停留在此，他会讲加法是人们能够进行的最简单、最基本的数的运算之一，减法实际上是加法的逆运算。乘法要复杂一些。作为一种运算，我们有两个数，并使用其中一个数来表示另外一个数的数量。如果愿意，你也可以认为这两个数分别是指矩形阵列的行数和列数。还有，乘法有对称性，例如 5×6=6×5，这是乘法运算的一个优美特征。然而，每个可以执行的操作几乎都需要能够撤销，在数学中更是如此。计算倍数有一个非常自然的逆过程，就是分割，这样的分割被称为除法。

洛克哈特的《度量》大开大合进展快速，而《算术的故事》则是细腻绵长。他会不厌其烦地讲述三位数乘法的每一个运算步骤，拼命让你记住怎么进位。洛克哈特说，我不是在讲怎么计数怎么运算，我是想让你从哲学和美学上理解算术。

洛克哈特认为，教数学课，最终是要让孩子领略到数学的美。孩子要有好奇心、游戏精神，并且能在想象力中愉悦自己。他在教程中引入数学史上的一些内容，就是要孩子面对人类曾经面对的一些基本问题，怎么计算，怎么度量。

数学中一个常见的悖论是，引入一个更高的理论，让原本看起来难的问题变得简单。比如我们小学课程中经常面临的一些应用题，一旦学会设未知数，就变得简单了。但我们的小学课程不讲未知数，洛克哈特的教学理念是从问题出发，不怕引入更高的数学概念，也不一定要割裂开几何和代数课。面对问题，解决问题，从一个问题到另一个问题，只有在这样的过程中，我们才能锻炼出真正的数学技巧。

《一个数学家的叹息》这本书，我讲完了。这本书的主要观点是，中小学数学课存在大量问题，让孩子掌握数学符号，记下一堆公式和定理，然后再不断做题，这种机械的教育不能让孩子领略数学的美，好的教育方式，是要让孩子置身于数学问题之中，由一个问题引向另一个问题，从中发展出数学思维和数学技巧。

这本书出版之后，有人发表评论说，这本书太好了，我的数学成绩就很差，如果我在中学里遇到一位像洛克哈特这样的老师，一定能学好数学。洛克哈特的确是一位好的数学老师，但他能不能把一个数学成绩很差的孩子，改变成一个对数学感兴趣的优秀学生，这需要打一个大大的问号。他的教学理念，适合那些聪明的孩子，但面对那些就是学不好数学的孩子，洛克哈特好像没什么高招。他说，中学并不能保证教会每个人基本的数学知识。

我觉得，他更像是一个数学兴趣小组的课外老师，领着一帮数学成绩好的孩子去领略数学的乐趣，并且对那些教不好数学的老师、学不好数学的孩子发出了长长的叹息。

撰稿：苗炜工作室解读脑图：刘艳导图工坊转述：徐惟杰

划重点

1. 洛克哈特的教育理念有一定的危险。你要跟着他学数学，应付中考高考，怕是会出问题。但是，如果你对数学感兴趣，愿意在数学中获得更多的乐趣，那洛克哈特会是一个很好的老师。

2. 中小学数学课存在大量问题，让孩子掌握数学符号，记下一堆公式和定理，然后再不断做题，这种机械的教育不能让孩子领略数学的美，好的教育方式，是要让孩子置身于数学问题之中，由一个问题引向另一个问题，从中发展出数学思维和数学技巧。