《议事的科学》 钱言解读
《议事的科学》| 钱言解读
你好,欢迎每天听本书,今天为你解读的是《议事的科学》。它能告诉我们,怎么在不同的决策场景中,选择最合适的议事方法,争取最优的决策效果。
比如,你有没有遇到过这样的情况:你和朋友们一起出去吃饭,大家都不知道该去哪里,于是你提议大家投票决定。但投票出来的结果是大多数人都不太满意,觉得自己的意见被忽略了。那么,有没有一种更好的方法,能够让大家都能接受,并且尽可能地满足每个人的偏好呢?
再比如,2016年,英国举行了一场具有历史意义的公投,决定是否脱离欧盟。结果是51.9%的人选择了脱欧,48.1%的人选择了留欧。这个结果让很多人感到惊讶和不满,甚至有人发起了重新公投的请愿。那么,这个结果真的反映了英国人民的真实意愿吗?如果换一种投票方式,结果会不会不同呢?
在这本书里,作者坦率地提出,“少数服从多数”可能导致不好的结果,因为多数表决并不能完全体现投票人的偏好,而且容易受到操纵和战略性投票的影响。因此我们要学习各种议事方法的原理,根据不同的情境和目标,选择最合适的决策方式,提高决策的质量。
这本书的作者坂井丰贵,是美国罗彻斯特大学经济学博士,日本新锐经济学家,开创了用大白话普及诺奖经济学理论的潮流。通过这本书我们能看到很多有趣的问题,比如英国公投脱离欧盟反映了英国人的真实意愿吗?美国总统大选的结果究竟合不合理?在世界上广为流传、被无数机构推崇的《罗伯特议事规则》有何漏洞等等。
通过分析这些问题,我们能了解很多重要的投票规则,比如多数表决、孔多塞规则、博尔达计数法等等,也能认识到这些方法的优缺点。能让我们在很多社会问题上增长见识,也能帮我们运用经济学思维,在工作和生活中取得更好的决策。
接下来,我就分两部分为你解读这本书。第一部分我们来看,什么是优秀的议事规则,为什么议事规则很重要;第二部分我们再看,在复杂的情况和博弈关系中,有哪些实用和高效的决策方法。
顺便说一句,这本书在得到站内的“顾衡讲好书”中曾经介绍过,其中顾衡老师重点讲述了从经济角度看待政治问题的局限性。而在今天的解读中,我们重点讲述投票规则对社会事务的重要性,以及用经济思维处理公共决策的实用性。希望听完之后,它能让你轻松学到一些新的知识,并且用经济学的思维方式,解决现实中的决策难题。
好,首先我们来看,什么是优秀的议事规则,为什么议事规则很重要。
说到这个问题,你可能会想,高质量的议事规则应该能反映大多数人的愿望,实现“少数服从多数”的原则,达成公平和民主。但是这本书告诉我们,优秀的议事规则并不是一成不变的,而是要根据不同的情境和目标来选择。有些时候,按多数表决并不是最好的方法,而是会导致悖论和操纵,所以采用什么样的议事规则很重要。
按多数表决带来的第一个问题,是票数分流。以2000年美国总统选举为例,民主党的戈尔和共和党的布什是两大党派的主要候选人。起初,戈尔似乎更有优势,但后来绿党的拉尔夫·纳德作为第三候选人插入战斗。他没有实力赢得选举,但他的大部分支持者也支持戈尔。因此,纳德抢走了部分原本属于戈尔的选票,给戈尔造成了重大打击,让布什反超并且获胜。
这场选举结果对全球格局产生了深远影响。2001年,布什当选总统后,美国遭受恐怖袭击。为了报复恐怖势力,布什于当年发动了阿富汗战争,2003年再次发动伊拉克战争。这场战争推翻了萨达姆,在伊拉克建立了民主政权,但并没有发现大规模杀伤性武器,萨达姆的残余势力还创建了极端武装组织“伊斯兰国”。可以说,决策方法改变了历史。
再比如,1860年的美国总统选举,共有四位候选人:共和党的林肯、北方民主党的道格拉斯、南方民主党的布雷肯里奇和宪政联合党的贝尔。林肯是唯一反对奴隶制的候选人,他在北方略胜一筹,但在南方却败得惨淡,全国总投票数还不到40%。他的主要对手道格拉斯支持奴隶制,布雷肯里奇的立场则比道格拉斯更倾向奴隶制,两人之间存在票源分流的问题。
按照政治学家里克尔的研究,只有通过多数投票才能让林肯获胜。如果没有布雷肯里奇参选,道格拉斯和他之间的选票分流就不会发生,道格拉斯就可能当选。因此,林肯的胜选实际上是利用了多数投票引发的选票分流。如果没有这种多数表决,林肯可能就会被淘汰,《解放黑人奴隶宣言》也就不会出现。
在这里,我们抛开政治立场不谈,可以看到在多数表决的选举中,多样的选择可能会使结果不能反映多数人的真实意愿,甚至影响历史的进程。那么,我们应该怎么办呢?
最简单的办法是对多数表决进行两轮投票。在第一轮投票中,如果没有人能得到半数以上的选票,就在得票最多的前两名中进行第二轮投票。如果使用这种方法,在2000年美国大选中布什和戈尔就会进入第二轮投票,最后可能会由戈尔获胜。这种方法叫做二轮决选,它可以让第一轮投票中分流的选票在第二轮投票中回流,从而避免错误。很多国家的政治选举经常采用这种方法。
例如,2002年的法国大选中,有16名候选人参加。在第一轮投票中,主要候选人之一的保卫共和联盟代表希拉克以19.9%的得票率排名第一,极右政党国民阵线代表勒庞以16.9%的得票率排名第二。被认为与希拉克实力相当的社会党代表若斯潘以16.2%的得票率排名第三。极右政党进入第二轮选举的事实震惊了欧洲社会,被媒体称为“勒庞危机”。这就是选票分流的结果。国民阵线没有与其政治立场相近的党派,因此它集中了右翼的选票。但在选票回流的第二轮投票中,希拉克以82.2%的得票率取得了压倒性胜利。这就是二轮决选的作用。
除了二轮决选,当选项多于三个时,还有一种方法是让选项两两对决,进行多数表决的循环赛。就像国际足联世界杯预选赛那样,让选项进行一对一的循环赛。如果有一个选项全胜,那么它可以说是真正的多数决胜者。但是,这种情况并不总是会出现。有时候很难判断谁才是真正的赢家,书中谈到了下面这个例子。
丹麦是一个议会制国家,它的国会议员是按比例代表制选举产生的,然后再由议员选举首相。由于有很多政党,首相通常是在多个政党的联合下组建执政联盟。在1994年的国民议会选举中,人们最看好的首相候选人有三位:已经在位的社会民主党的拉斯穆森、自由党的外交部长乌夫·埃勒曼-延森,还有保守人民党的法务大臣恩格尔。最终,拉斯穆森与其他两党组建的执政联盟得以存续,他也连任首相。
但是,一家调查公司就公众对三名候选人的看法进行了民意调查,结果发现在谁更受欢迎的问题上,三人之间出现了奇妙的循环。该公司将三名候选人两两对决,分别询问“在这两个人中,你更支持谁”,也就是让三个人进行了一场多数决的循环赛。结果是拉斯穆森击败了恩格尔,恩格尔击败了埃勒曼-延森,但埃勒曼-延森又击败了拉斯穆森。就像石头剪刀布一样,三人互有胜负,无法确定谁最受公众欢迎。这就是所谓的投票悖论。
那么,如何解决投票悖论呢?为了便于理解和记忆,我们用一个虚拟的中国学生干部选举的例子来说明。假设三位候选人小明、小华和小丽为了竞选学生会干部,进行两两辩论,并接受观众投票,投票结果是这样的:
结果一:小明对小华,小明以80票对50票胜出。
结果二:小华对小丽,小华以110票对20票胜出。
结果三:小丽对小明,小丽以70票对60票胜出。
现在我们看到,小明击败了小华,小华击败了小丽,但小丽又击败了小明,这就是投票悖论。怎么解决这个问题呢?一个办法就是剔除得票差最小的一场。我们可以去掉结果三,然后根据结果一和结果二来得出“小明、小华、小丽”的顺序。这就像在足球比赛中需要考虑净胜球,选举也需要考虑得票差。
这个方法的依据是,结果一的得票差是30票,结果二的得票差达到了90票,而结果三的得票差只有10票,小丽赢得非常侥幸。所以,我们就剔除了结果三 。这个方法是由18世纪法国学者孔多塞首创的,所以叫孔多塞原则。但遗憾的是,这个方法只在选项不超过4个的情况下有效,超过4个选项,投票悖论还是存在。
投票悖论的存在意味着,会议的审议流程会对结果产生很大影响。如果会议主持人能判断参会者的选择,那么他就可以通过调整提案的顺序来达到自己想要的结果。
比如在上面的例子中,虽然存在投票悖论,但小丽明显不太受欢迎。因为在结果三中,小丽只是以微弱的优势赢了小明。然而,如果主持人偏爱小丽,只要他调整审议流程,小丽就有可能赢。他可以先让小明和小华进行投票,然后小明以80票对50票胜出。然后他让小明和小丽进行投票,小丽以70票对60票胜出。这样小丽就赢了。
如果主持人希望小明或小华赢,他也可以用这个办法。这样,主持人就成了某种意义上的独裁者,他想让谁赢就谁赢,而且他还可以用多数表决掩盖他的目的,使大家都不容易发现。
这就让我们看到了罗伯特议事规则的问题。这个议事规则非常有名,它遵循一个原则——和草案对抗的修正案只能有一个。为了确定最终修正案,需要先对不同的修正案进行表决,然后再和草案进行表决。这样一来,发言顺序会影响修正案的制定,而不是根据所有选项的排序来决定。这可能导致投票悖论,也就是所有计数法下的赢家却无法被选中。
由此我们可以看到,不同的决策方法会带来不同的结果,有时甚至会出现人为的操纵。为了防止这种情况,我们需要同时对所有选项投票,而不是分别投票;并且不能只用简单的多数表决,因为那样会产生票源分流的问题。那么,有没有更好的办法,来避免这些问题和缺陷呢?
这就是接下来我们要说的,怎么在复杂的情况和博弈关系中,选择实用和高效的决策方法。
在这本书里,作者介绍了很多实用的决策方法,包括博尔达计数法、中位数选项法、沙普利值评估等等,其中最重要的是博尔达计数法。
这种方法是由法国科学家博尔达在18世纪提出的,它规定选民可以在选票上同时填写第二位、第三位,甚至第四位、第五位候选人,可以避免选票分流的问题。
例如,在选举中如果有五个选项,排在第一名的将得到5分,第二名得到4分,第三名得到3分,第四名得到2分,最后一名得到1分。所有选民的选票分数加起来,最后得分最高的选项获胜。
比如在2000年美国总统大选中,如果采用二轮决选,布什和戈尔会进入第二轮投票,最终戈尔会赢;如果采用博尔达计数法,戈尔的得分理应高于其他两名候选人,戈尔也会赢。
可见,博尔达计数法和二轮决选都可以抑制选票分流的影响。但区别在于,博尔达计数法更简单高效。它们的差异在于对待第二位以下被支持者的方式。
比如有一个候选人,在所有选民心中都排第二。如果采用多数投票,他甚至无法进入前三名;如果采用二轮决选,他还是排在最后,因为选民只能在选票上填写最支持的候选人;但是,如果采用博尔达计数法,这个候选人得分最高,就会当选。
从全票通过的角度考虑,如果所有人都把某个人作为自己首位支持的对象,那么多数表决、二轮决选或博尔达计数法都会选择他。但是当无法实现全票通过时,博尔达计数法能选出更接近全票通过的候选人。
作者在书中论证了,在一个有四个候选人的案例中,如果把每个选民将候选人提升到第一位所需要的步数,看作是他到达全票的距离,那么博尔达计数法选择的候选人离全票通过的距离最短。所以,博尔达计数法更符合最多数人的民主原则。
正因为如此,博尔达计数法得到了广泛的认可和应用。
比如政治选举。选民可以通过博尔达计数法对多个候选人进行排名。然后将所有选民的分数加起来,最高分的候选人获胜。这种方法在新西兰地方选举以及中欧斯洛文尼亚的少数民族代表选举中都有应用。
再比如体育竞赛。在艺术体操、冰上舞蹈等体育项目中,裁判对选手的表演进行排序并赋予相应的分数,最后分数最高的选手获胜。
再比如科研投入。研究人员可以根据自己的判断为不同的研究项目排名,然后根据排名为每个项目计分,以此确定应该优先投入哪些项目。这都是博尔达计数法的应用。
当然,博尔达计数法也可能受到战略性投票的影响。如果投票者了解其他投票者的选择,他们可能会调整自己的投票,以增加他们最喜欢的选项赢得投票的可能性。
但即便如此,在作者看来,博尔达计数法依然是一种出色的决策机制。因为它定义简单,容易被大众理解,我们很容易在实践中进行应用。
除此之外,这本书还介绍了一种决定费用分摊的方法——沙普利值评估法,也很有参考价值。
你可能听说过,在很多地方,小区居民会因为维修电梯的费用分担问题,闹得沸沸扬扬,僵持不下,比如书中提到了这么一件轶事。
有一栋五层公寓的电梯需要维修,但谁付钱成了问题。一楼的人几乎不用电梯,因此不愿付钱。然后呢,五楼的人突然出了个馊主意,说让一楼的人全包了,结果在二楼到五楼的人支持下,这个提议居然以80%的票数通过了。当然,这是个虚构的故事,从中可以看到多数表决被滥用的尴尬。因为每层住户受益不同,把费用全推给一楼显然很不公平。所以,电梯维修的费用该怎么分摊,还真是个问题。
现在让我们换一种方式来看这个问题。想象一下,有三家航空公司,A公司的飞机小,B公司的中等,C公司的飞机大。为了满足这三家公司的需求,机场必须建一条能让C公司的大飞机起降的长跑道。这条跑道分成三部分:A部分是所有公司都用的,要花12亿元;B部分是B和C公司用的,要花6亿元;C部分只有C公司用,要花5亿元。总共需要23亿元。
那么,怎么公平地分配这23亿元的建设费用呢?首先,把A部分的12亿元均分给三家公司,每家负担4亿元。接着,B部分需要增加的6亿元,分给B和C公司,每家负担3亿元。最后,C部分增加的5亿元,全部由C公司承担。这样,每家公司的支付额就是A公司4亿元,B公司7亿元(也就是4亿+3亿),C公司12亿元(等于4亿+3亿+5亿)。这就是沙普利值的计算方法,它能确保每家公司支付的金额和它从跑道中获得的利益相符,公平合理。
把这个思路应用到电梯维修问题上。同样地,电梯的使用和楼层的高低有关,我们也可以依据沙普利值分摊维修费用。比如,一楼的住户几乎不用电梯,他们应该承担的费用就比较少;五楼的住户更依赖电梯,他们就应该承担更多的费用。
但是说到这儿,问题还没完。因为电梯的运行,不仅给住在高层的居民带来了便利,让他们可以快速上下楼,而且还增加了整个公寓的价值。即使住在一楼的居民不常使用电梯,他们也从电梯的存在中获得了收益,这是他们的共同利益。这么看来,该如何公平地分摊电梯维修的费用呢?
我们可以考虑两个方面,一个是每层住户从电梯中获得的便利性,这部分可以使用沙普利值来计算;另一个是电梯对整个公寓价值的提升,这部分费用应该由所有住户均摊。
现在假设有一栋三层的公寓,电梯维修费用总额是48,我们首先计算沙普利值。假设一到二层的维修费用是36,由二楼和三楼各自承担18;二层到三层的维修费用是12,全部由三楼承担。这样一来,一楼负担0,二楼负担18,三楼负担30。
接下来,我们要考虑公寓价值提升这个部分。我们假设总费用的一半,也就是24,按照均摊原则来分配。这样每层都需要承担8的费用。然后,我们将沙普利值的计算结果减半,一层还是0,二层是9,三层是15。最后把均摊和减半的沙普利值加起来,得出结果:一楼是 8+0=8;二楼是 8+9=17;三楼是 8+15=23。这就是按照50%的比例,把沙普利值和均摊结合起来的结果。
这种方法被称为“凸组合”,即使沙普利值和均摊的比例变了,也可以用同样的方法计算出每层该承担的费用。
但是问题还没完,它还有一个难点,就是怎么决定沙普利值和均摊的比例。比如,我们是应该让维修费用全部按照均摊,也就是沙普利值占比0%,还是全部按照沙普利值,也就是沙普利值占比100%?我们如何决定这个比例呢?
可能有人觉得电梯的便捷性和它对公寓价值的提升同样重要,所以提议沙普利值和均摊各占50%。也可能有人认为每层的住户都享有电梯的使用权,所以建议沙普利值的占比应为0%。这种比例很难只根据理论原则来决定,我们需要找到一个最容易被大家接受的结果。
现在假设每个人心里都有一个最喜欢的比例点。如果比例低于这个点,他们会觉得沙普利值太低了;如果比例高于这个点,他们会觉得沙普利值太高了。我们叫它峰值。怎么从这些峰值中选一个大家都能接受的比例呢?
一个不太好的方法是算峰值的平均数。比如,三个人的峰值是10%、30%、50%,平均数就是30%。但是如果有人故意说一个很极端的数,比如100%,就能影响结果。比如,10%、30%、100%的平均数是46.7%,和他心里的峰值很接近。
而更好的方法是选中间的峰值。如果三个人的峰值是10%、30%、50%,就选30%;即使变成10%、30%、100%,还是选30%。这样就算有人故意说极端的数也没用,就避免了有人通过提出极端值来影响决策结果。
这就是所谓的中位数选项。这个选项在和其他任何选项比较时都更有优势,因此它是全胜者。全胜者代表了大多数人的意见,而且中间选项容易让大家觉得是互相让步的结果,也更容易让大家接受。这样一来,我们就在复杂的利益博弈中,找到了相对可行的方法。
说到这儿,关于这本书的解读就接近尾声了,我们来回顾一下。这本《议事的科学》,是日本新锐经济学家坂井丰贵的作品,它借用众多诺贝尔经济学奖得主的思想,介绍了很多重要的投票规则,我们可以从中学习各种议事方法的原理和效果,根据自己的需要选择最合适的决策方式。
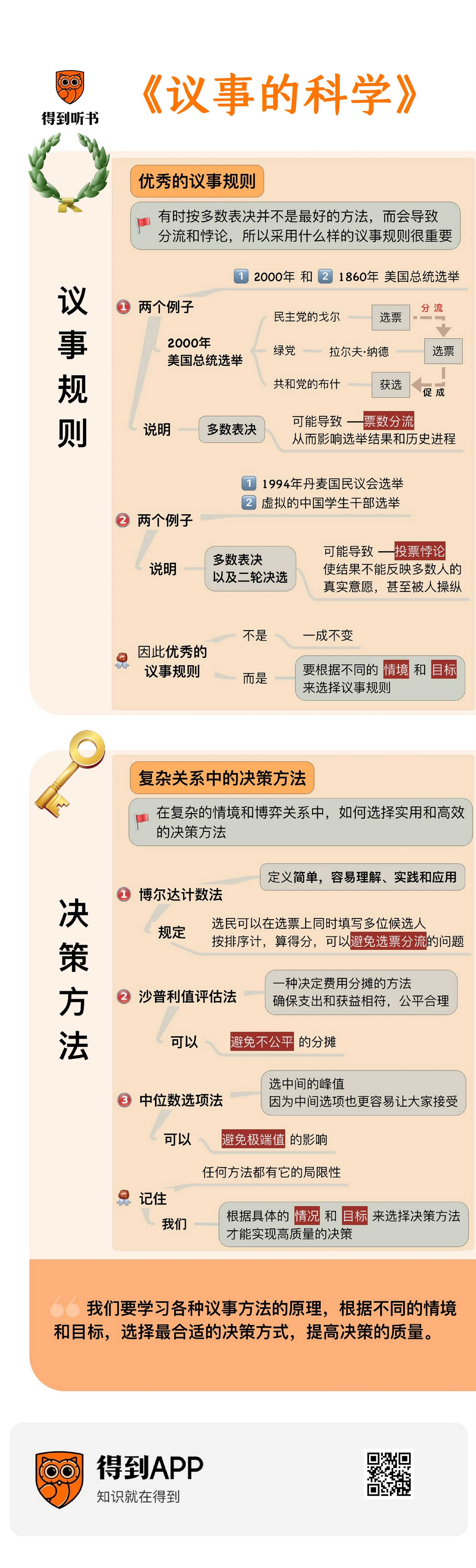
在第一部分,我们介绍了什么是优秀的议事规则,为什么议事规则很重要。我们通过2000年美国总统选举和1860年美国总统选举两个例子,说明了多数表决可能导致票数分流,从而影响选举结果和历史进程。我们还通过1994年丹麦国民议会选举和一个虚拟的中国学生干部选举的例子,说明多数表决以及二轮决选可能导致投票悖论,使结果不能反映多数人的真实意愿,甚至被会议主持人操纵。因此我们可以认识到,优秀的议事规则并不是一成不变的,而是要根据不同的情境和目标来选择。
在第二部分,我们介绍了在复杂的情境和博弈关系中,如何选择实用和高效的决策方法。其中最重要的是博尔达计数法,它规定选民可以在选票上同时填写多位候选人,按排序计算得分,可以避免选票分流的问题。并且它定义简单,容易被大众理解,很容易在实践中应用。此外,我们还通过公寓电梯维修费用分摊等案例,介绍了中位数选项法和沙普利值评估法。中位数选项法可以避免极端值的影响,沙普利值评估法可以避免不公平的分摊,它们都是很重要的决策机制。不过我们要记住,任何方法都有它的局限性,我们要根据具体的情况和目标来选择,才能实现高质量的决策。
特别值得一提的是,在本书最后,作者用议事规则引出了几个发人深省的问题。比如,如果两个男人想要决斗,我们应不应该尊重他们的意愿?如果两个朋友因为宗教信仰而互相干涉,我们应不应该尊重他们的感受,等等。作者觉得,并不是所有心里的自由都应该得到社会的尊重。如果人们的内心欲望会侵犯到他人的自由,那么我们更应该优先保护每个人的自由权益,而不是实现他们内心的想法。这样才能做到,每个人都有机会走上他们认为会带来幸福的道路,并自己承担因此产生的结果。这才是人生决策的最大原则。
好,以上就是这本书的解读。你可以点击音频下方的“文稿”按钮,查收我们为你准备的全文和脑图;还可以点击右上角的“分享”按钮,把它免费分享给你的朋友;最后还附上了这本书的电子书链接,欢迎你去拓展阅读。恭喜你,又听完了一本书。
划重点
-
优秀的议事规则并不是一成不变的,而是要根据不同的情境和目标来选择。有些时候,按多数表决并不是最好的方法,而是会导致悖论和操纵,所以采用什么样的议事规则很重要。
-
博尔达计数法是一种出色的决策机制,因为它定义简单,容易被大众理解,我们很容易在实践中进行应用。中位数选项法可以避免极端值的影响,沙普利值评估法可以避免不公平的分摊,它们都是很重要的决策机制。
-
不过我们要记住,任何方法都有它的局限性,我们要根据具体的情况和目标来选择,才能实现高质量的决策。