《心中有数》 哈希解读
《心中有数》|哈希解读

开头
你好,欢迎每天听本书,我是哈希。今天我要为你解读的这本书,名叫《心中有数》,副标题是“生活中的数学思维”。
这本书的作者叫刘雪峰,是北京航空航天大学计算机学院的副教授,主要研究方向包括线性代数、信号处理、人工智能。他写的这本《心中有数》,获得了第十八届文津图书奖,入选了豆瓣2022年度科学新知图书。
既然是2022年出版的书,显然不算新书了。那为什么现在才解读呢?因为过去两年它都被我束之高阁了。主要就是因为这书名里的“数学”两个字。我向来对数学是“能逃则逃”,所以就迟迟没有翻开它。
但是前阵子一个偶然的机会,我翻开了它,竟然一读就被吸引住了:原来解决数学题的思路可以迁移到这么多的人生选择题中!在管理大小项目时,是应该追求“尽善尽美“,还是学会“委曲求全”?是应该“步步为营”,还是“精益求精”?在生活中,应该更注重频繁的“小确幸”还是偶尔的“大幸福”?年轻时应该多去闯荡,还是坚守赛道?对于这些问题,还有其他更多的问题,数学思维都能够给出它的回答,而且很多时候出人意料。
希望今天这本书,也能够给你一双看世界的新眼睛。
用可控的弊,换取更大的利
我们先来看这么一道题:地图上有7个城市,每两个城市之间的距离是已知的,现在让你求出一条经过所有城市,并且最终回到出发点的距离最短的路线。
这个问题其实应用非常广泛,小到餐厅送餐,邮递员送货;大到几个城市之间工业运输路线的规划,背后都是这类问题。
你可以暂停想一想,你有没有什么好方法应对这类问题呢?
一个坏消息是,数学家从理论上证明,要想找到最优路线,没有什么简便方法,只能暴力穷举,就是把所有的路线都列举出来,然后分别计算长度,才能找到那条最短的。
但是,用这种方法,有一个致命的缺点是,你要耗费的时间会随着节点数量的增加而急剧增加。7个城市的话,一共就有720种排列方式,就是要算720次;这也还好,但是要是稍微增加到10个城市,排列方式就会猛增到362880种;如果有26个城市,排列方式的数量就有1.5×10的25次方这么多,这已经远远超过科学家估测的宇宙中所有恒星的数量了。
在计算机科学中,科学家们给这类问题起了个专有名字,叫NP难问题(NP-hard problem)。这里的“难”不是指没有办法解决,而是指,找到最优解所需要的时间,会随着问题规模的扩大而急剧增加。
而在现实中,规划路线涉及到的节点数量,可能有成百上千个。就更是难上加难了。
那么,该怎么解决呢?
对此,计算机科学家设计了很多的启发式算法。简单来说,这种算法可以帮助我们得到一个接近最优解的解。
比如,还是开头那7个城市最短路线的问题,有一个简单的启发式算法叫“最近邻居法”,就是:从任何一个城市开始,每访问的下一个城市都是距离当前城市最近、同时尚未被访问的城市。
虽然最后你得到的这个解,可能不是最优解,只是一个近似最优解,但它的优势在于,计算出解的速度比穷举法要快得多。
另外,计算机科学家在设计一个启发式算法的时候,可以额外地实现一个效果,就是限制最优解和用启发式算法找到的解的比值。什么意思呢?很简单。比如说,有一个启发式算法的近似比是2,那就意味着,这个算法找出的解对应的距离,在最差的情况下不会超过最优解对应的距离的2倍。
可能我们会质疑了:既然你都不知道最优解是什么,你怎么保证最后不超过它的2倍呢?这确实看起来很神奇,但是,在数学上确实是可以做出这样的保证的。
那么,我们可以从这样的启发式算法中,获得什么启发呢?
那就是,当我们很难达到理想结果的时候,应该学会用“可控的弊”换取“更大的利”。
在寻找最短距离这个问题当中,“可控的弊”就是一个误差范围可控的近似最优解,“更大的利”就是更快的计算速度。
而像这样,用“可控的弊”换取“更大的利”的思想,在实际生活当中也有很多的应用。最直接的,比如,人们经常说的“先完成再完美”;还有,用一点利益让步换取长久合作,或者舍弃局部保全大局,等等。
再比如,在美国,森林野火每年都造成很严重的破坏。过去很多年,他们的应对政策是“野火必救”:就是一旦在野外发现小火苗,就立刻派人扑灭。但这种方法似乎没有降低发生大规模森林火灾的概率。后来,美国林务局在一个生态学家的建议下,修改了野火治理政策,不再实施“野火必救”。也就是说,在一些小火苗燃起的时候,先不扑灭,而是主动在可控范围内,让野火把枯木还有其他的易燃物一起烧掉,这样反而能避免因为累积过多的枯木而造成不可收拾的大火。结果,这样做之后,大规模森林火灾发生的概率明显降低了。
还有,兵书中有一个被称为“围城必阙”的心理战术,是指在攻城的时候,不要把城池全部包围起来,而是打开一个缺口让敌人逃跑。这是因为,如果敌军深陷重围,无处可跑,觉得没有活路,就必定会拼死抵抗,不好降服。而放开缺口,虽然可能会放跑少数的敌人,但是带来的好处是,能够瓦解敌人的士气,更好降伏。这些都属于是主动用可控的弊,换取更大的利。这是当最优解很难取得的时候,解决问题的一个有效策略。
频繁的小确幸与偶尔的大幸福
下面我们再来看一个距离我们生活更近的数学思想。我们想想这么一个问题:偶尔的大幸福和频繁的小确幸,哪种更能使我们感到幸福呢?
小确幸有哪些?比如:早上醒来,发现自己养的植物开花了;出门一按电梯,电梯门就正好开了;开车的时候,你在的这条车道最顺畅;打开购物软件,突然发现购物车里一直没舍得买的商品降价了,等等。这些都是小确幸,是生活当中小小的幸运和快乐。
与小确幸对应的是“大幸福”。比如升职加薪、结婚生子、彩票中奖、金榜题名,等等,这些都是大幸福。
那么,偶尔的大幸福和频繁的小确幸,哪种更能使我们感到幸福呢?
之前我们在解读《有钱,能买到快乐吗?》那本书的时候,提到过经济学家们的一个研究结论:频繁的小额消费,会带来比一次大额消费更多的快乐。这似乎跟这个问题有些类似。那么从数学的视角来看,答案也会是类似的吗?
先说答案:还真是。不过,它的应用场景比我们想象的要更广泛。
书里在这里涉及到一个“卷积”的概念。我们不用去深入理解它,可以就简单地记住,卷积的目的是刻画一个系统对于外界输入的反应。比如,你身体不舒服,吃了药。假设你的身体是系统,那么这个药就是输入,而你的身体变化,就是输出。再有,你到办公室,被老板表扬了,那么这个表扬就是外界的输入,而你产生的心情变化就是你对于这个输入的输出。
这些输入其实都可以看作是外界环境对我们的系统发出的刺激,这种单次的刺激在控制系统中被称为“冲激函数”。而系统受到冲激函数作用后的输出,通常是:从零开始升高,到达最高点后再慢慢下降,直到为零。也就是像一座小山,或者是一个波浪一样。这很好理解,就比如面对一个表扬,我们先是心情突然变好,然后再慢慢平复。这也像一个波浪一样。
那么,如果输入并是一次性的刺激,而是会持续一段时间呢?
在数学中,我们需要把这个连续的输入信号,拆解成一系列的冲激函数,也叫脉冲序列,类似于不断地、密集地给刺激。而卷积,说的就是:系统对于一个脉冲序列的响应,就是它对单独每个脉冲输入的响应的叠加。类似于,一波未平,一波又起,而这波与波之间又靠得很近,那你的心情就相当于是每一波的影响的叠加。
我们可以用卷积来说明这个大幸福和小确幸对幸福感的影响。
显然,不管是大幸福还是小确幸,它们都是一种冲激函数。它们作用在“你”这个系统上,会让你产生幸福感。但是这种感觉不会持续很久,会很快消退。
美国进化心理学学者罗伯特·赖特曾经在他的著作《洞见》当中,从生物进化的角度分析了为什么会这样。我们人类努力做的很多事情,包括吃到好吃的、战胜对手、找到伴侣等,这些行为有助于我们传播自己的基因。进化让我们的大脑在实现这些目标的时候能够产生快感,在这些快感的驱使下,我们才会不断追寻这些目标。但是,进化心理学又告诉我们,这些快感不应该持续很久。毕竟,如果努力成功了一次之后带来的幸福感不会消退,那么我们就会一直沉浸在这种幸福感里,没动力去追求更高的目标了。
那么,如果我们把大幸福和小确幸带来的幸福感都看作是波浪的话,那么大幸福带来的显然就是大波浪,小确幸带来的就是小波浪。但是从卷积的角度来看,一连串频繁发生的小波浪,它们的影响叠加之后,反而会让你整体的幸福感在相对长的时间里一直处于高水平。我在文稿里放了一张示意图,有空时你可以点开看看。
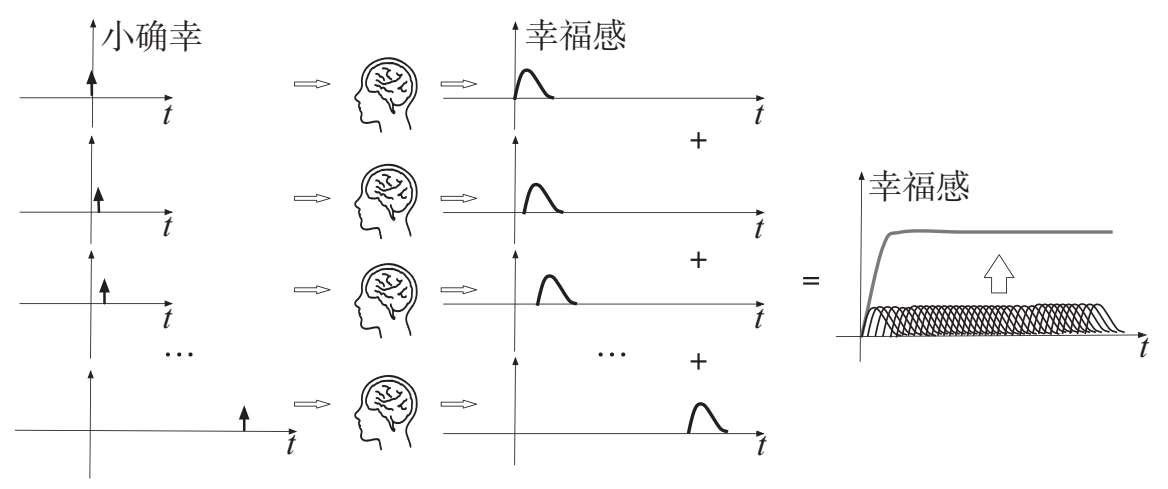
这其实也能跟我们之前解读的那本《有钱能买到快乐吗?》联系起来。为什么像通勤、打扫、人际交往这些小事,它们对于我们幸福感的影响程度,竟然超过了升职加薪,住上大房子等等这些一次性发生的大变化。因为那些小事是我们每一天都要经历的,它们决定了我们日常的小确幸。
我们当然不是要否认大幸福的作用。但是这个数学思想提醒了我们,如果我们的人生只是期盼着下一个大幸福,却忽视了身边的小确幸的话,我们可能在人生的更多时候都处于幸福感的低谷,只有偶尔能够达到波峰;但如果我们能够注意到日常的小确幸,珍惜小确幸,甚至有意识地经常给自己制造小确幸的话,那么就能够平衡幸福感的波动,让自己处在更好的日常状态中。
如何寻找人生最优解?
好,下面呢,我们再来看一类经典的人生场景,也是跟数学问题交集很大的一类场景,就是寻求最优解。可以是项目管理、产品研发中的最优解,也可以是人生规划中的最优解。
我们借用一个数学里面求最优解的典型场景,就是求一个函数的最大值。比如,这是一个二次函数,它的形状是一个像小山一样的抛物线。那么,怎么求它的最大值?
最直接的显然是求导法。我们知道,它总共就是三步:(1)求导数,(2)让导数为零,(3)找到方程的解。
虽然步骤简单,但是要得到正确的结果,你每一步都不能出错。这种模式对应一个成语,就是:“步步为营”。它要求每一步都要完美,把整个流程走完,才能得到想要的结果。
这就是一种我们上学的时候最常用的方法,也可能是当时我们最坚信的理念——每一步都要力求完美。但是,在步入社会之后,我们很可能会发现,这种思路没有那么好用了。因为很多时候,你做不到每一步都是最优的。
这个时候我们其实可以参考另外一种解法,叫数值解法。
还是假设我们面对的是一个形状像小山的二次函数图像。那么,要找到这个函数最大值的位置,我们可以先随便猜一个x的值,代入进函数,得出一个函数值。然后,我们在x的附近试数,如果试了下一个比x更大一点的数,代进函数计算,函数值上升了,那我们就可以再试一个更大一点的数,以此类推;如果得出的函数值比之前的要小,那我们就再后退一点儿,找一个小一点的数,继续试。不断重复这些步骤,就可能得出最大值所在的位置。
这就是数值解法。从数学上看,跟求导法相比,数值解法不需要知道函数的具体表达式,也不要求函数处处可导。所以,在科学工程当中如果需要找函数极值,绝大部分时候会采用这种方法。现在在深度神经网络领域,都是采用这种思路来训练神经网络的参数。
那么,从更广泛的意义上,数值解法能给我们什么启发呢?
你肯定已经感受到,数值解法的思路并不是试图一次就找到函数最大值的位置,不像求导法一样要求在每一步都做到精确,而是通过逐步的迭代不断地逼近那个最大值。
如果迁移到产品开发上,求导法跟数值解法其实对应的是两种思路。
一个产品的开发流程当中有多种不同的模型,其中的一种常见的模型是瀑布模型。它把一个产品的开发分为需求分析、设计、实现、发布等多个阶段。各个阶段按照固定的次序衔接,就像形成瀑布的流水一样,逐级下落。所以叫“瀑布模型”。
瀑布模型的思想,就很像求导法的“步步为营”。你看,产品开发被明确地分为几个阶段,要在完美地完成前一个阶段后才能进入下一个阶段。最后一个阶段的任务完成后,就可以得到最后的理想结果。
但是,用瀑布模型来开发产品,有两个重要的缺点。
第一,这样的开发流程不适应用户需求的变化。因为用户需求在最前端,一旦用户需求发生变化,整个开发流程全部需要从头再来。
第二,只有在项目生命周期到了后期,你才能看到结果。
书里讲到一个真实的例子。老王是一个公司高管,也是一个足球爱好者。他经常苦于踢足球时临时组不成队,所以他就有了一个做个足球社交平台的想法。在这个平台上,人们可以组队订场去踢球。他越想越觉得这个想法很有前景,所以他就辞了工作,投入多年的积蓄,组建开发团队,全情地投入研发这个应用。
他们在研发过程中为了尽善尽美、优化用户体验,开发了很多的功能,开发进度比预期慢了很多,但老王认为这是必需的。因为他认为只有推出一个“完美”的产品到市场,用户才会买单。在整整开发了一年之后,让老王比较满意的“完美”应用终于完成了。
但是,等到他们把这个应用投放市场后发现,虽然这个应用是免费的,但是几个月过去,下载的人非常少。可能是市场并没有这个需求?或者是产品还有很多可以优化的地方?没有人说得清楚为什么。总之这个项目最后不了了之了。
老王的这种产品开发模式就是使用了典型的“瀑布模型”。就像我们前面说的,这个模型最大的问题就是,他们在把自己觉得完美的产品推向市场之前,没法知道用户反馈。那么很可能出现的情况就是,投入了大量的资源、金钱、时间,开发出来了,结果没人买单。
而跟这个瀑布模型相对的是敏捷模型(Agile Model)。在用敏捷模型开发产品的时候,整个开发工作被组织为一系列短周期的快速迭代。每一次迭代都包含了需求分析、设计、实现与测试工作这些所有的流程,并且通过客户的反馈不断地进行改进,直至达到最后的要求。这就很像是数值解法的思路,就是不试图在每一步都做到完美,而是迅速走完一轮,然后在这一轮结果的基础上迭代,反复好多轮,不断地提高,最后也可以得到一个好结果。
很显然,和瀑布模型相比,用敏捷模型做产品开发,有这么两个突出的优势:
第一,敏捷模型的短周期迭代思想,可以很好地适应用户需求的变化。
第二,能够快速得到早期用户的反馈,然后对产品进行改良。
这也类似很多公司经常说的“要先有‘最小可行产品’(Minimum Viable Product,MVP)”或者“小步快跑,快速迭代”。
这种思路还可以用在写文章或者写论文上。书里用写论文来举例:写一篇论文有两种模式。
第一种模式是“求导法”的思路,步步为营。先琢磨一个完美的想法,然后做实验验证,等实验做完,拿到了所有数据再开始写。
第二种模式是“数值解法”思路,快速迭代。稍微有了一个初步可行的想法就开始写,写的时候不太打磨语言细节,用最快的时间写出一个初稿。写完给周围人看,让他们提意见,然后针对这些意见改进想法、用实验验证想法,修改文章。甚至可以在刚有提纲的时候就开始请周围人提建议。这样,经过多轮迭代,完成对文章的打磨。
包括作者在内的很多资深的研究工作者,都会建议年轻学者采用第二种思路,也就是“数值解法”思路。先尽可能地写出一个“可行但不完美的论文”,然后不断地迭代来改进。
刚才我们对比了求导法和数值解法。求导法,我们上学的时候最常用;面对简单规整的函数,它也最好用。而走上社会,面对更加复杂的项目,面对不断变化的需求或形式,数值解法就变得比导数法更实用了。
但是,如果迁移到整个人生呢?你看,我们刚才设想的都是有一道小山丘一样的函数形状,去求最优解。但是,我们真实的人生总是起起伏伏的,它不是一座山丘,而是重峦叠嶂。从图像上看,像一条接连不断,高高低低的波浪线。它有多少个波峰,多少个波谷?波峰有多高,波谷有多低?我们提前并不能知道。这种情况,怎么寻找最优解呢?
还用数值解法,可行吗?
就不太可行了。为什么呢?因为,站在数学的角度来说,当函数形式比较复杂的时候,用数值解法可能会陷入局部的最高点。比如,我们设想一下,眼前这条波浪线的形状像两个山丘,它有两个高点,第二个点更高。那么,如果我们以第一个高点的山脚位置为起点来试数,经过多次迭代之后,一定会收敛到第一个较矮的高点处,也就是局部最高点,而不是全局最高点。
那么,怎么解决呢?我们琢磨一下,数值解法之所以会让我们困在局部最高点里,跳不出来,是因为它的想法是:你只有每一步都比上一步更高,才觉得我们是在朝着一个好的方向走;只要这一步比上一步低了,就不接受,就要掉头离开。
所以要跳出困局,关键就在于,如果处在局部最高点的时候,我们可以接受它右侧位置更低的点,那么从这个点开始迭代,就可以跳出局部最高点,到达全局最高点。
如果切换到人生场景,数值解法之所以会让我们困入局部最高点,是因为它不能接受短期的挫折,每一步都要追求眼前有利可得。而想要跳出来,关键就在于,能接受暂时的不太完美,用暂时的不完美来换取一个更好的未来。
这就好比,很多人在换工作时,都要求下一份工作的工资比当前更高,感觉这样才是往上跳。但是,如果新公司的行业前景更好,那么暂时的薪资退步也不应该是完全不能接受,因为这是为了以后能达到更高的高度。
那么,我们还可以继续追问,我们该以什么样的方式接受不完美?
书里介绍了一种模拟退火算法。先说说这个奇怪的名字是怎么来的。你可能在影视作品里看见过这样的场景:一个铁匠正在反复敲打一个烧的很红的兵器,然后从炉火里把它拿出来,放进水里,只听见“呲”的一声,升起一阵白雾。这叫“淬火”,是快速让金属冷却。
但是退火跟淬火不一样,退火的冷却速度比淬火要慢得多。退火是通过缓慢地降低金属的温度,来增加材料的延展性和韧性。
所以,退火的核心就是三个字:慢慢来。这也是模拟退火算法的核心思想。只不过它慢慢降低的不是金属的温度,而是对于不完美的概率的接受程度。
具体来讲,在刚开始的时候,我们要接受这一次试的数得出的结果有比较大的概率不如上一次。而越往后,我们通过算法设计,逐步降低对于这个不完美的概率的接受程度。
这就是模拟退火算法。它告诉我们,在开始的时候,我们要接受结果有较大的概率并不完美,而这个概率,会随着时间的推移慢慢降低。
那么,迁移到人生场景呢?它能给我们什么启发呢?
作者认为就是,越是年轻的时候,越应该接受更大的随机性,更大的不完美概率。这对应着,年轻的时候要多去闯一闯,多尝试不同的机会,进而找到自己的兴趣、发现自己的潜力。
而模拟退火算法进一步告诉我们,这个随机性应该随着你的年龄慢慢降低。当你年轻的时候,你可以让这个随机性较大,充分探索外界,让自己接受暂时的不完美,好在将来跃上一个更高峰。而在年龄渐长、知道自己最适合什么之后,就要控制随机性,在自己最适合的地方深耕,不轻易切换赛道。
结语
好,以上,就是这本书里,我想跟你分享的重点内容。
人生就是一个不断寻找最优解的过程,也是一个不断寻找更高效策略解决现有问题的过程。而这也是许许多多的数学思维想要达成的目标。今天,我们讲了很多能够迁移到生活场景中的数学思维。除了这些以外,书里还探讨了其他的一些有趣的问题,比如,应该相信“人各有命”还是“事在人为”?“勤能补拙”真的是对的吗?“三个臭皮匠,顶个诸葛亮”有没有道理?感兴趣的朋友,推荐你去读读原书。
愿你“心中有数”,行之有方。
好,今天这本书,我们就聊到这里。你可以点击音频下方的“文稿”,查收这本听书的全文还有脑图。原书电子版,已经为你附在了文稿末尾,欢迎你进行拓展阅读。你还可以点击右上角的“分享”按钮,把这本书免费分享给你的朋友。
恭喜你,又听完了一本书!
划重点
1、解决NP难问题时,不应执着于找到最优解,而是用启发式算法寻找近似最优解,用可控的误差换取更快的计算速度。
2、在实际生活中,当最优解很难达到时,不要固执地追求完美,而要学会用"可控的弊"换取"更大的利"。
3、从卷积的角度看,频繁的小确幸带来的幸福感,不会像偶尔的大幸福那样昙花一现,而是能在相对长的时间里维持在高位。
4、年轻时要像"模拟退火算法"那样多尝试,接受更大的随机性,而随着年龄增长,应该逐步降低随机性,深耕最适合自己的领域。